Термин «скорость» может использоваться в различных областях, например, в физике, термодинамике, химии и т.д. Прежде чем мы продолжим рассмотрение линейной и угловой скорости, сначала дадим определение скорости как отдельного термина.
Линейная скорость: формула нахождения
С точки зрения физики, не существует такого понятия, как абсолютный покой. Каждое тело и частицы, из которых оно состоит, находятся в постоянном движении относительно друг друга. Наиболее важной кинематической величиной, характеризующей движение, является скорость. В этой статье приведены формулы линейных скоростей для различных типов тел, движущихся в пространстве.
Это физическая величина, которая показывает, какое расстояние в пространстве проходит тело за единицу времени. Скорость обычно обозначается буквой v¯, а дефис указывает на то, что это векторная величина. Скорость измеряется в метрах в секунду (м/с), километрах в час (км/ч), милях в час (миль/ч) и других единицах, которые показывают связь между расстоянием и временем.
Это вас заинтересует: «Время от времени»: путаница или разлука? Как правописание зависит от типа слова?
Вектор скорости v¯ указывает направление фактического движения тела. Это отличается от вектора ускорения, который указывает в направлении действующей силы, но не в направлении движения тела, хотя эти два вектора могут совпадать.
Мгновенная и средняя скорости

Как можно определить линейную скорость? Формула может быть записана следующим образом в соответствии с определением количества:
Где dl¯ — вектор смещения тела в момент времени dt. Эта скорость называется мгновенной, потому что она вычисляется для чрезвычайно короткого промежутка времени dt. Мгновенная скорость на самом деле является нестабильной и постоянно меняющейся величиной. Например, предположим, что автомобиль движется по дороге. Легко поверить, что мгновенная скорость постоянна во все времена. Мгновенная скорость изменяется. Если спидометр автомобиля достаточно чувствителен, он будет регистрировать эти изменения.
Это вас заинтересует: Базальная неоплазия в раннем детстве: общая особенность развития ребенка
Формула для средней линейной скорости не отличается от формулы для мгновенной скорости, но она измеряется за более длительный промежуток времени Δt:
v¯ = Δl¯/Δt, где Δt>>дт.
В приведенном выше примере с автомобилем мгновенная скорость колеблется, но средняя скорость в некоторой степени постоянна на протяжении всего расстояния Δl¯.
Обычно для решения задач используется средняя скорость. Мгновенное значение имеет смысл только при движении с ускорением.
Равномерное движение по прямой линии
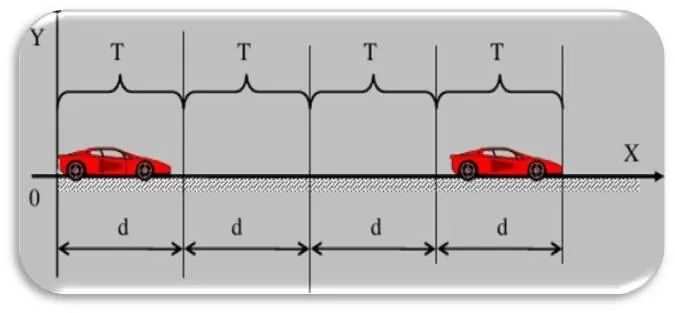
Это идеализированная форма движения, при которой предполагается, что тело движется в течение определенного времени по прямой линии в пространстве. Скорость тела не меняется. Если мы обозначим пройденное расстояние символом l, то получим формулу:
Этот тип движения рассматривался уже философами Древней Греции. Они предположили, что на тела, которые должны двигаться, должна действовать сила, поэтому естественным состоянием всех окружающих их объектов является покой. Только в эпоху Возрождения, благодаря работам Галилея и Ньютона, было доказано, что равномерность и прямолинейность движения тела не нарушается, если на него не действуют внешние силы.
Формула для расчета линейной скорости

Мы с детства интуитивно воспринимаем скорость. Например, когда мы смотрим в окно или стоим на улице, мы замечаем, что одни люди ходят быстрее других, а машины на проезжей части едут быстрее любого пешехода. Однако для физики как науки такого повседневного понимания скорости недостаточно, поэтому вводится точное определение.
Понятие скорости
Скорость материальной точки (тела) при равномерном движении — это физическая величина, показывающая, на какое расстояние точка (тело) перемещается в единицу времени.
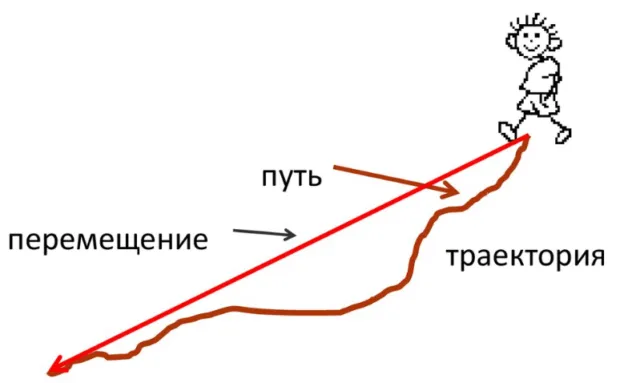
Следует подчеркнуть, что речь идет именно о расстоянии, а не о перемещении. Перемещение — это вектор, соединяющий начальную и конечную точки движения. Его значение равно расстоянию между этими точками. Путь — это длина траектории, по которой происходило движение. Графически это можно показать на рисунке.
Равномерное движение — это движение, при котором тело проходит одинаковое расстояние за одинаковые промежутки времени. Направление движения может меняться. Примером может служить равномерное движение точки по окружности.
Формула для понятия скорости выглядит следующим образом:
\\overline<\mathrm>=s / t\
На одну строку выше заголовка<\mathrm
На одну строку выше заголовка<\mathrm
Из приведенной выше формулы очень легко определить меру скорости. Поскольку расстояние измеряется в метрах, а время — в секундах, единицей измерения скорости являются метры в секунду м/с. Обратите внимание, что на практике скорость часто измеряется не в метрах в секунду, а, например, в километрах в час.
Существует также так называемая средняя скорость, скалярная величина, которая соответствует скорости, с которой тело могло бы двигаться, если бы преодолевало одно и то же расстояние.
Поезд длиной 300 м, движущийся с равномерной скоростью, проходит через туннель длиной 420 м за 3 минуты. Найдите скорость поезда.
Решение: Обозначим длину поезда через l, а длину тоннеля через L. Фраза «проходит тоннель за 3 минуты» означает, что на этот раз поезд въезжает в тоннель с кабиной машиниста и выезжает в конце последнего вагона. Тогда пройденное расстояние S равно сумме длины туннеля и длины поезда. \S = I + L = 300 + 420 = 720 м/с.\Скорость поезда — это скорость любой из его точек. Для простоты предположим, что это скорость движения кабины водителя. Переводим минуты в секунды: 3 * 60 = 180 с. Скорость получается путем деления расстояния на время: 720/180 = 4 м/с.
Ответ: Скорость поезда равна 4 м/с.
Автомобиль движется со скоростью 4 км/ч в течение 3 часов, а затем со скоростью 61,2 км/ч в течение 4 часов. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение. Найдите общее расстояние, пройденное автомобилем. Он обозначается S. Итоговое значение равно сумме расстояний, пройденных автомобилем со скоростью 58,4 км/ч и 61,2 км/ч. Назовем первое из этих расстояний \S_\, оно равно \S_\ = 3*58,4 = 175,2 км. Назовем второе S2, оно равнозначно. Общее время t, которое она прошла, равно \t = t_ + t_ = 3 + 4 = 7 ч/ Чтобы найти среднюю скорость, разделите общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.
Линейная скорость
Линейная скорость — это величина, которая соответствует расстоянию, пройденному телом за единицу времени. Движение тела может быть линейным или идти по криволинейной траектории, например, по окружности. Обратите внимание, что линейная скорость всегда направлена по касательной к траектории.
Существует множество формул для расчета линейной скорости, но одна из них является общепринятой:
\v=S / t\
S — расстояние, пройденное телом, t — время, затраченное на это.
Если тело вращается по кругу, то расстояние, которое оно проходит, равно его длине. Как известно из геометрии, эта величина равна 2πR, где R — радиус круга. Отсюда легко вывести, что линейная скорость тела, равномерно движущегося по окружности, равна \\\boldsymbol\.
У вас нет времени, чтобы решить проблему самостоятельно?
Сложение скоростей
Скорость — это векторная величина. Если материальная точка участвует в нескольких движениях, ее скорость определяется как векторная сумма скоростей отдельных движений:
В некоторых случаях полезно представить сложное движение как суперпозицию нескольких простых движений. Тогда уравнение (6) можно рассматривать как правило разложения вектора скорости на составляющие.
Примеры задач с решением
Задание. Вектор изменения радиуса, определяющий положение материальной точки, задается уравнением: $\overline\left(t
ight)=t^4\overline+3t^2\overline,$где $\overline$ и $\overline$ — единичные векторы осей X и Y (Рисунок 2). Какова мгновенная скорость точки в момент времени $t=1$c?
Решение. Определите скорость частицы как:
Подставляя в формулу (1.1) уравнение для радиус-вектора $\overline\left(t
ight)=t^4\overline+3t^2\overline,$ получаем:
\overline=\frac\left(t^4\overline+3t^2\overline
ight)=4t^3\overline+6t\overline\\left(1.2
ight).\
Из уравнения (1.2) видно, что:
Согласно теореме Пифагора, коэффициент скорости можно рассчитать следующим образом:
Мы вычисляем скорость, подставляя в полученную формулу время $t=1$c:
\v\left(t=1
Какая формула линейной скорости?
ight)=\sqrt\approx 7,2\left(\frac
ight).
Ответ. $v$=7,2 $\frac$
Задание. Материальная точка движется по прямой линии. Ускорение этой точки возрастает, как показано на диаграмме (рис. 3). Какова скорость точки в момент времени $t_1?
Решение. На графике (рис. 3) ускорение представлено прямой линией, исходящей из начала координат. Исходя из рис. 3, мы записываем аналитическое выражение для ускорения следующим образом: