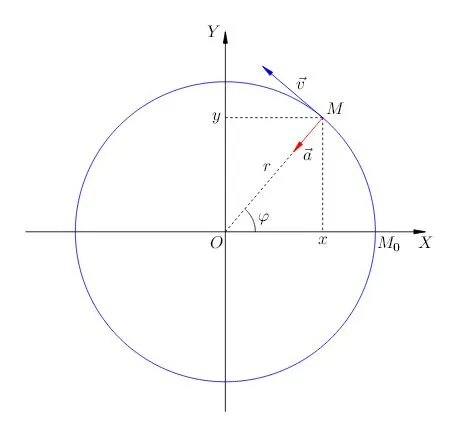
Общий угол поворота объекта в любой момент времени можно определить по графику угловых перемещений. Чем круче график, тем выше мгновенная угловая скорость в данный момент времени.
Равномерное движение по окружности.
Задача с датчиком USE: круговое движение с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное круговое движение — это довольно простой пример движения с вектором ускорения, зависящим от времени.
Предполагается, что точка вращается вокруг окружности радиуса. Скорость точки постоянна по модулю и равна Эта скорость называется линейной скоростью точки.
Орбитальный период — это время полного оборота. Существует очевидная формула для этого периода.
Частота движения является обратной величиной периода.
Частота показывает, сколько оборотов в секунду совершает точка. Частота измеряется в об/с (оборотах в секунду).
Например, предположим, что. Это означает, что точка совершает полный оборот. Частота в данном случае равна r/s-, что означает, что точка совершает 10 оборотов в секунду.
Угловая скорость.
Считайте, что точка равномерно вращается в декартовой системе координат. Поместите начальную точку координат в центр круга (рис. 1).
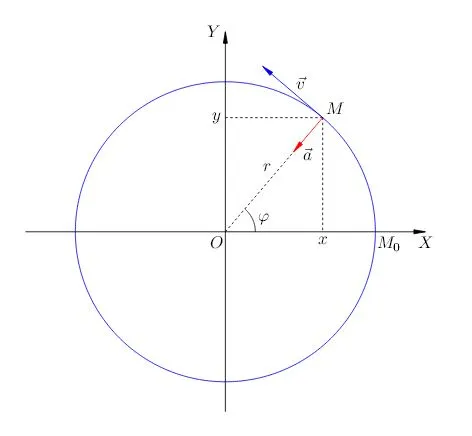 |
| Рис. 1.Равномерное движение по окружности |
Предположим начальное положение точки, т.е. если точка имеет координаты. Поверните точку на определенный угол с течением времени, а затем продолжите.
Отношение угла поворота ко времени называется угловой скоростью вращения точки.
Углы обычно измеряются в радианах, поэтому угловая скорость измеряется в радианах/секунду. В течение времени, равного периоду вращения, точка поворачивается на определенный угол. Поэтому.
Объединение уравнений (1) и (3) дает зависимость между линейной и угловой скоростью.
Центростремительное ускорение.
Теперь нас интересует ускорение точки вращения. Его можно найти, выделив отношение дважды (5): .
Полученное уравнение (6) можно записать в виде векторного уравнения
где — радиус-вектор точки вращения.
Видно, что вектор ускорения направлен в сторону, противоположную радиус-вектору, то есть к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительной силой.
Кроме того, из уравнения (7) мы получаем выражение для измеренного значения центростремительного ускорения.
( Выразите угловую скорость из (4)
( Замените его на (8). Мы получаем другое выражение для центростремительного ускорения.
Если; — угловое смещение в радиальных единицах, s — длина дуги, ограниченной с обеих сторон углом поворота, r — радиус, в зависимости от определения радиуса
Формулы для нахождения линейной скорости
Если скорость объекта характеризуется постоянной величиной, то объект движется равномерно. Формула для расчета скорости этого движения такова
где s — пройденное расстояние, т.е. длина линии.
t — время, за которое тело прошло по заданному пути.
Линейная скорость V — это физическая величина, которая указывает на расстояние, пройденное объектом за определенный период времени.
Основным уравнением для определения линейной скорости является следующая формула
t обозначает время, за которое тело прошло путь S.
Другой вариант уравнения имеет вид
t обозначает время, затраченное телом на прохождение дуги l.
В некоторых научных источниках скорость обозначается строчной буквой v. Другим уравнением для расчета линейной скорости является уравнение
В данном случае 2π представляет собой полный круг, 360 градусов. Вектор скорости направлен по касательной к траектории тела.
Модуль скорости
Арифметическое значение скорости может отличаться в зависимости от выбранной единицы измерения. Помимо численного значения, скорость характеризуется также ее направлением. В физике численное значение скорости называется ее коэффициентом.
Если скорость имеет определенное направление, то она является вектором. Поэтому скорость — это естественный размер вектора. Измерение скорости записывается как v, а вектор скорости как ⌘ (⌘ vec \).
Следует отметить, что такие величины, как маршрут, время и длина, встречаются только в числовых значениях. Они называются фазовыми величинами. Если тело движется неравномерно, то справедливо использовать в расчете среднюю скорость.
Задачи с примерами решения
Тело движется по кругу с ускорением 3 м/с в квадрате. Радиус окружности равен 40 метрам. Необходимо определить линейную скорость движения тела.
В этом случае ускорение является нормальным. Исходя из этого, вы можете определить линейную скорость тела, используя следующие виды
Ответ: линейная скорость равна 10,9 м/с.
Поезд движется равномерно. Он преодолевает расстояние в 219 км за 4 часа. Вам нужно рассчитать скорость поезда.
Используя базовый тип для расчета линейной скорости, вы получаете
ОТВЕТ: скорость поезда составит 54,75 км/ч или 15,2 м/с.
Автомобиль с двигателем внутреннего сгорания преодолевает расстояние в 213 км/ч за 2,5 часа. Необходимо определить скорость автомобиля.
Используйте уравнение для расчета скорости и запишите решение задачи.
ОТВЕТ: скорость перемещения составляет 85,2 км/ч или 23,7 м/с.
Скорость вращения курсора напрямую связана со скоростью вращения магнитного поля статора. Поле создается тремя обмотками, установленными под углом 120°.
Число оборотов
Все скорости вращения характеризуются частотой вращения n или эквивалентной частотой f. Оба размера описывают количество оборотов в единицу времени.
Si единицы частоты (или оборотов)
В технике скорость обычно измеряется в направлениях в минуту (об/мин) = 1/мин.
Поэтому обратная величина числа оборотов — это продолжительность вращения.
Если n — число витков, f — частота, а t — продолжительность вращения, период. Это угловой сдвиг, где n — общее число оборотов, а t — время, период вращения. Затем существует угловая частота
ограничение
Угловой сдвиг.
Равен ли угловой сдвиг произведению общего числа скоростей?
Угловая скорость
Из уравнения для вращения можно получить следующие результаты
Примечание: — Данный тип применим ко всем видам вращательного движения — как к равномерному, так и к ускоренному движению. Может включать фиксированные, средние, начальные, конечные и немедленные цены. — В отличие от своего названия, количество оборотов n — это не число, а натуральная величина. — Следует различать количество витков и общее количество витков n.
Равномерное движение тела по окружности
Когда угловая скорость постоянна, говорят, что тело движется равномерно и одинаково. То есть тело вращается на один и тот же угол через равные промежутки времени.
; — угловая скорость (фиксированная во времени); — угловое смещение t — является ли время поворота углом?
На графике угловой скорости площадь прямоугольника соответствует угловому сдвигу, поэтому есть
Постоянная угловая скорость — это отношение углового перемещения (угла поворота) к времени, необходимому для его перемещения.
Единицы СИ угловой скорости:.
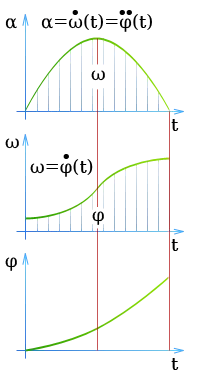
Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно увеличивается.
? -это мгновенная угловая скорость объекта в момент времени t. — постоянное угловое ускорение в момент времени t. -это угловое смещение тела в момент времени t (в радиусе?). t — время.
На диаграмме скоростей угловое перемещение равно площади треугольника, поэтому: ?
Как изменяется угловая скорость, когда тело начинает вращаться из состояния покоя? равна угловой скорости, достигнутой в результате ускорения? Таким образом, уравнение становится.
Количество повторений события или его возникновение в единицу времени называется частотой. Это физическая величина, измеряемая в герцах (Гц). Он обозначается буквами ν, f и F и представляет собой соотношение между количеством повторяющихся событий и продолжительностью, в течение которой они происходят.
Движение по циклоиде*
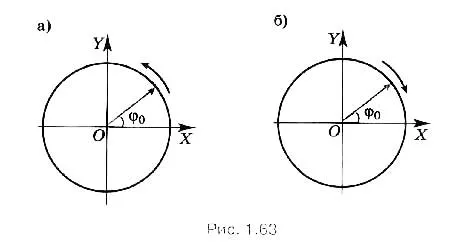
В системе отсчета, связанной с колесом, точка вращается равномерно со скоростью в пределах окружности радиуса R, причем скорость изменяется только по направлению. Центростремительное ускорение точки направлено к центру окружности по радиусу.
Теперь перейдем к стационарным системам, связанным с землей. Поскольку ускорение не меняется при переходе от одной инерциальной системы отсчета к другой, полное ускорение в точке A остается одинаковым как по модулю, так и по направлению. С точки зрения неподвижного наблюдателя, траектория точки A уже не окружность, а более сложная кривая (циклоида), точки которой движутся неравномерно.
Это означает, что чем больше радиус окружности, по которой движется точка B, тем больше значение ускорения по модулю. Чем дальше точка твердого тела находится от оси вращения, тем больше его ускорение.
Угловая скорость и угловое ускорение
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела.
Угловая скорость — это скорость вращения объекта, которая определяется увеличением угла поворота объекта за определенный период времени.
Имя: ω (омега).
Виды угловой скорости.
В зависимости от заданных параметров вращения формула для расчета угловой скорости выглядит следующим образом.
- Обороты в единицу времени об/мин, с-1.
- Угол поворота в единицу времени, рад/с.
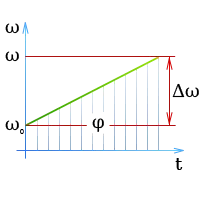
Скорость изменения угла φ (смещение из положения P).1 Должность P2) — угловая скорость: c-1.
Например, угловая скорость объекта, вращающегося со скоростью 1,5 оборота в секунду, равна
Если k — положительная аксиальная единица авс, то
Вектор угловых скоростей — это вектор скольжения. Он может быть применен к любой точке на оси вращения и всегда ориентирован вдоль оси. Положительные значения угловой скорости совпадают с направлением ω и k, а отрицательные значения — это Напротив.
Угловое ускорение
Угловое ускорение — это скорость изменения угловой скорости при вращении твердого тела.
Единицы измерения углового ускорения: рад / с 2, с -2.
Векторы углового ускорения также отображаются вдоль оси вращения. При ускоренном вращении они движутся в одном направлении, а при замедлении — в противоположном.
Другими словами, положительное ускорение увеличивает угловую скорость, а отрицательное — замедляет вращение.
Для некоторых особых случаев вращательного движения твердых тел можно использовать следующее уравнение
-
равномерное вращение ( ω — const )
В технике угловая скорость часто указывается в оборотах в минуту nrpm. Один оборот составляет 2π радиуса:.
Уважаемые студенты! На нашем сайте вы можете получить помощь по техническим и другим вопросам: ✔ Задачи и решения тестов ✔ εξετά экзамен помощь в изучении конспектов

Решение задач, контрольных и РГР
При необходимости вы можете добавить файлы или фотографии своей работы.
Вы будете проинформированы о цене в течение пяти минут на указанный вами адрес электронной почты.
Если вас устраивает цена, вы можете оформить заказ.
Учебные комплекты для студентов.
-Учебная коробка A4 -Различные цвета -Шрифт ГОСТ (государственный стандарт) -Шифрованные и полосатые рабочие листы
Спящий лев вращается полностью, как Земля вращается вокруг своей оси. Земля делает это за период времени, равный одному дню. Таким образом, период вращения составляет один день. Количество секунд в сутках: 1 сутки = 24-60-60 секунд = 86400 секунд = 86,4∙103 секунды.
Переход от угловой к линейной скорости
Существует разница между линейной и угловой скоростью точки. Сравнивая значения уравнений, описывающих правила вращения, мы можем увидеть сходство между этими двумя понятиями. Каждая точка B, принадлежащая окружности радиуса R, проходит путь, равный 2*π*R. Таким образом, он совершает революцию. Поскольку время, необходимое для этого, составляет период T, значение модуля линейной скорости точки B может быть найдено следующей операцией
Учитывая ω = 2*π*ν, мы имеем
Таким образом, линейная скорость точки B увеличивается по мере удаления точки от центра вращения.
В целях повествования. Если в качестве таких точек рассматривать города на широте Санкт-Петербурга, то их линейная скорость относительно оси Земли равна 233 м/с. Для объектов на экваторе она равна 465 м/с.
Численное значение вектора равномерного ускорения точки B выражается через R и угловую скорость следующим образом
α=ν2/R, где ν=ω* R. Подставляем α=ν2/R=ω2*R.
Это означает, что чем больше радиус окружности, по которой движется точка B, тем больше значение ускорения по модулю. Чем дальше точка твердого тела находится от оси вращения, тем больше его ускорение.
Таким образом, ускорение, скорость и их положение в любой требуемой точке тела могут быть рассчитаны в любой момент времени.
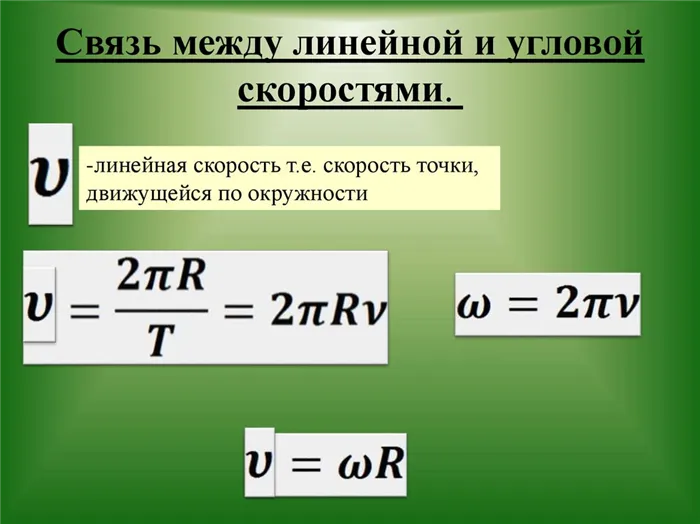
Понимая и умея пользоваться расчетами и не путая определения, вы сможете вычислять линейные и угловые скорости и свободно переходить от одного размера к другому.