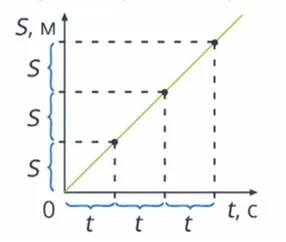
Тело брошено под углом α = 90° к горизонту. Другими словами, тело запускается вертикально вверх с начальной скоростью V0. Ось x направлена вертикально вверх так, чтобы ее направление совпадало с вектором начальной скорости. F — сила тяжести, направленная вниз. В первый момент времени тело находится в точке A.
Как найти скорость зная среднюю скорость
Автор и опытная группа исследователей внесли свой вклад в эту работу и проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 8. Их список можно найти внизу страницы.
Команда управления контентом wikiHow внимательно следит за работой редакторов, чтобы каждая статья соответствовала установленным высоким стандартам качества.
Чтобы рассчитать среднюю скорость, используйте следующую простую формулу: скорость = затраченное время>>.< ext>>>. Однако некоторые задачи дают две скорости, одну для разных частей пройденного расстояния, а другую — для разных периодов. В таких случаях для расчета средней скорости необходимо использовать другие формулы. Вам может понадобиться умение решать такие задачи в реальной жизни, или у вас могут возникнуть проблемы на экзаменах, поэтому выучите формулы и поймите принципы решения задач.
На этой странице вы можете использовать калькулятор для расчета вашей средней скорости интернета. Для расчета введите расстояние и время.
Средняя (путевая) скорость — это отношение длины пути, пройденного объектом, ко времени, затраченному на прохождение этого пути.
Через расстояние и время
Формула для нахождения средней скорости, зная расстояние и время:.
Этот видеоурок доступен по подписке.
У вас уже есть подписка? Войти.
В предыдущем уроке мы рассмотрели равномерное движение. В этом уроке мы рассмотрим движение с переменной скоростью, или неравномерное движение. Вы также узнаете о характеристиках неравномерного движения: средней скорости и мгновенной скорости.
Введение
Мы рассмотрим несколько типов трафика.
-колебания груза на маятниковой пружине (рис. 1); -колебания груза на маятниковой пружине (рис. 1); и
Рисунок 1.Колебания нагрузки на маятниковой пружине (источник.)
-Раскачивание тела по наклонной плоскости (рис. 2),.
Рис. 2.- Скользящий крен кузова (источник)
Рис. 3. Свободное падение (источник).
Все три движения не являются однородными. То есть, они связаны с изменением скорости. В этом уроке мы рассмотрим неравномерные движения.
Неравномерное движение
Равномерное движение — это механическое движение объекта, когда он проходит одно и то же расстояние за одно и то же время (рис. 4).
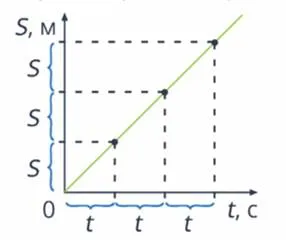
Рисунок 4: Равномерное движение
Неравномерное движение — это механическое движение, когда объект перемещается через равные промежутки времени на неравные расстояния.
Рис. 5.Неизомерное движение
Основная проблема в инженерном деле — определение положения тела в любой момент времени. Поскольку неравномерное движение изменяет скорость тела, необходимо научиться учитывать изменения скорости тела. Для этого вводятся два понятия: средняя скорость и мгновенная скорость.
Компьютерными веб-сайтами может пользоваться любой человек, имеющий подключение к Интернету и веб-браузер с поддержкой Flash. Регистрация или ввод персональных данных в предлагаемые такими службами услуги не требуется. Система автоматически вычисляет ответ.
Ответ
Найти Л. Разделите путь (как показано на рисунке) на три части (0-1 секунда, затем 1-4 секунды, затем 4-5 секунд).
1. s = Vot (начальная скорость за время) + at²/ 2; a (ускорение) = ΔV/Δt = 15 м/с²
3. S =Vot+at²/2; a=ΔV/Δt= -15м/с² (торможение тела)
Этот видеоурок доступен по подписке.
У вас уже есть подписка? Войти.
Другими словами, ускорение — это величина, определяемая изменением скорости за время, в течение которого происходит это изменение.
Опять же, каково равновесное ускорение?
Автомобиль за каждую секунду увеличивает свою скорость на
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением
Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение
Уравнение скорости снаряда имеет следующий вид
Это уравнение позволяет определить скорость в любой момент движения тела. Что касается закона изменения скорости во времени, то необходимо учитывать направление скорости относительно выбранной СО.
О направлении скорости и ускорения
При равномерном движении направление скорости и перемещения всегда одно и то же. Для равномерного ускорения направление скорости не обязательно совпадает с направлением ускорения, а направление ускорения не обязательно указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения
1. скорость и ускорение направлены в одну сторону вдоль прямой линии (рис. 1).
Рис. 1.Скорость и ускорение направлены в одну сторону вдоль прямой линии
В этом случае тело ускоряется. Примерами такого движения являются свободное падение, запуск и ускорение автобуса или запуск и ускорение ракеты.
2. скорость и ускорение направлены в разные стороны вдоль прямой линии (рис. 2).
Рисунок 2.Скорость и ускорение направлены в разные стороны вдоль прямой линии
Этот тип движения иногда называют эквидистантным движением. В этом случае говорят, что организм замедляется. В конце концов, он останавливается или начинает двигаться в противоположном направлении. Примером такого движения является камень, брошенный вертикально вверх.
3. скорость и ускорение взаимно перпендикулярны (рис. 3).
Рисунок 3. Скорость и ускорение взаимно перпендикулярны друг другу
Примерами таких движений являются движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случае орбита движения является круговой.
Поэтому направление ускорения не всегда совпадает с направлением скорости, но всегда с направлением изменения скорости.
График скорости
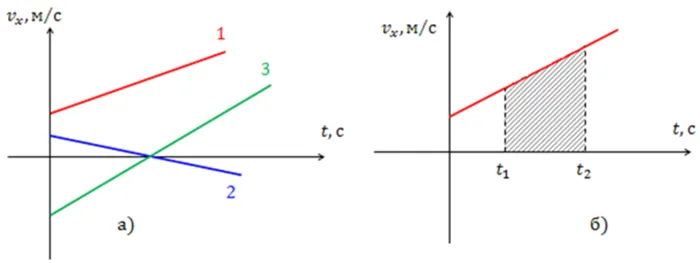
График скорости (проекция скорости) — это закон изменения скорости (проекции скорости) от времени для последовательных линейных движений, представленных графиком.
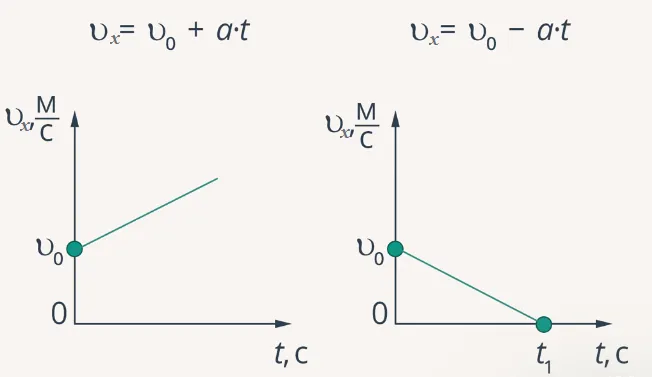
Рисунок 4.Диаграмма зависимости между проекцией скорости и временем для равномерного прямолинейного движения
Анализируя различные графики, мы видим, что первый — это проекция скорости движения.
Первый. Уравнение проекции скорости:
Вторая — зависимость от отрицательного значения проекции ускорения при замедлении движения, т.е. при первом уменьшении единиц скорости. В этом случае уравнение становится
График начинается в точке
Где

Рис. 5. График функции
Это линейное уравнение, что подтверждается рассмотренными графиками.
Конечно, свободное падение возможно не только на Земле, но и вблизи тел достаточной массы. У других мультяшных тел падение также плоское, но величина ускорения в свободном падении отличается от земного. Кстати, в прошлом были статьи о гравитации.
Равноускоренное движение
Если положение тела изменяется относительно неподвижного объекта с течением времени, говорят, что оно движется. В этом случае скорость используется в качестве основного параметра для описания движения. Движение тела или точки можно представить в виде линии, идущей по траектории. Это называется траекторией. Если линия прямая, то и движение прямолинейное.
Неравномерные движения характеризуются движением по разным траекториям с разными значениями скорости. В этом случае изменение положения может быть ускорено одинаково. Это означает, что параметры одного и того же интервала увеличиваются или уменьшаются на одно и то же значение. Примером может служить падение камня.
В любой данной точке скорость перемещения равна ускорению силы тяжести.
Поэтому, если вектор V и ускорение A следуют по прямой линии, то это направление можно рассматривать как алгебраическую величину в проекции. При равновесном движении вдоль прямой линии скорость точки рассчитывается по следующему уравнению: V = V0 + A*t. Где.
- V0 — начальная скорость, и
- A — ускорение (постоянная величина), и
- t — время движения.
Это основное уравнение физики. На графике она отображается в виде прямой линии v(t). Ось ординат — время, а ось лимба — скорость. Построив график, можно определить ускорение в точке A по наклону линии. Для этого найдите сторону треугольника по формуле: a = (v-v0)/t.
Если рассматривать интервал Δt на оси времени, то можно предположить, что движение равномерно и описывается параметром, равным мгновенному значению в середине интервала. Это мгновенное значение является векторным значением. Это численно равно пределу, который пытаются достичь в период, когда скорость стремится к нулю. В физике это состояние описывается уравнением мгновенной скорости: v = lim(Δs/Δt) = r — 1(t). Другими словами, с математической точки зрения, это первая производная.
Отсюда можно сказать, что движение Δs = v*Δt. Поскольку произведение ускорений на время определяется разностью V-V0, то правильной будет следующая запись: S = V0 * t + A * t 2/2 = (V 2-V 2 0)/2*A.
Из этого уравнения можно получить выражение для конечной скорости точки массы: V = (V 2 0-2 * A * s)½. Если начальный момент V 0 = 0, то уравнение можно упростить до следующего вида: V = (2 * A * s)½.
Среднее значение
В кинематике средние параметры используются для нахождения свойств. Он используется для изучения движения материальной точки или любого физического тела. Для определения средней скорости используются две величины: градуированная и векторная. Первый относится к перемещению пути, а второй — к перемещению.
Скорость движения определяется как отношение пройденного объектом расстояния к времени, необходимому для его прохождения: V=Σs/Σt.

На практике среднее значение — это среднее арифметическое всех скоростей за одно и то же время прохождения точки. В противном случае определяемое значение является средневзвешенным арифметическим.
Математически формула для средней скорости записывается следующим образом: v(t +Δt) = Δs/Δt= (s(t +Δt) — s(t))/Δt. Поскольку Δs зависит от длины пути, пройденного точкой за время Δt, правильная запись: Δs= s(t +Δt) — s(t). Если требуемое время стремится к нулю, то получается то же уравнение, что и для мгновенной скорости.
Вектор масс находится отношением положения тела к промежутку времени: V(t +Δt) = Δr/Δt= (r(t +Δt) — r(t))/Δt, где r — вектор радиусов. Если объект совершает равномерное линейное движение, то применяется следующее уравнение: =V.
Например, мяч катится со скоростью 20 секунд на первой половине дистанции в 100 метров и с другой скоростью в течение одной минуты. Необходимо рассчитать среднюю скорость. Согласно формуле, расстояние, пройденное на первой части маршрута, равно t1 = s / 2 * V1, а расстояние, пройденное на второй части, равно t2 = s / 2 * V2. Решение задачи: Vcf = s/(t1 + t2) = s / (s / 2 * v1 + s / 2 * v2) = 2 * V1 * V2 / (V1 + V2) = 100 / (20 + 60) = 1,25 м/с.
Угловая скорость
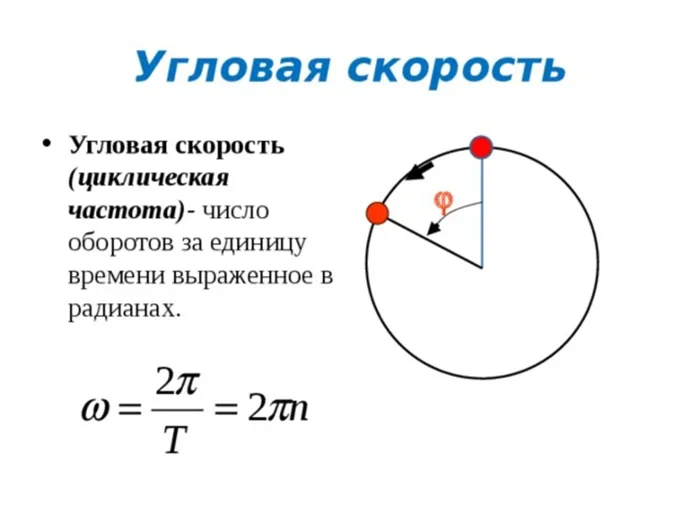
Это происходит, когда тело вращается вокруг оси. Орбита является круговой. Основным параметром, учитываемым при его нахождении, является угол поворота (f). Все основные угловые движения являются векторами. Нормальное вращение равно углу поворота df объекта за короткое время dt в направлении, противоположном движению часовой стрелки.
В математике уравнение для нахождения углового параметра записывается как w = df/dt. Угловая скорость представляет собой осевое значение вдоль мгновенной оси и совпадает с поступательным вращением правого винта. Равномерное вращение, т.е. движение, при котором поворот происходит на один и тот же угол, называется равномерным. Измерение угловой скорости определяется следующим уравнением: w = f / t, где f — угол поворота, а t — время, в которое произошел поворот. Поскольку Δf = 2p, уравнение можно перефразировать в w = 2p / T. Другими словами, используется период.
Существует зависимость между угловой скоростью и количеством оборотов: w = 2 * p*v. Это понятие используется для решения задач при описании неравномерных вращений. Существует также уравнение, связывающее линейную скорость с угловой: v = w* R, где R — компонент, отложенный перпендикулярно вектору радиусов. В качестве единицы измерения используется радиус, деленный на секунды (рад / с).
Например, определите угловую скорость преобразователя, когда подвешенная масса перемещается на 10 метров. Радиус руки равен 40 см. В первый момент подвеска неподвижна, а затем начинает опускаться с ускорением A = 0,04 м/с2 .
Поскольку линейная скорость преобразователя совпадает с линейным движением груза, мы можем написать V = (2 * a * S)½. Ответ: V = (4 * 0,04 * 10) ½ = 1,26 м/с. Угловая скорость находится по следующему уравнению: w = v / R, R = 40 см = 0,4 м, W = 1,26 / 0,4 = 3,15 рад/с.