Движение происходит повсюду вокруг нас, будь то падающий с крыши кубик льда, тормозящий на остановке автобус или несущийся со скоростью сноубордиста по склону. У этих примеров есть нечто общее: кубик льда, автобус и сноубордист движутся с ускорением. Давайте узнаем, какие формулы и графики позволяют описать движение с ускорением.
Все формулы ускорения. Виды ускорения
В физике, при изучении механического движения, скорость и ускорение являются двумя наиболее важными величинами, на которые следует обратить внимание. Знание их связи со временем позволяет нам определить координаты тела в пространстве в любой момент времени. В этой статье мы приведем все различные виды ускорения для разных типов ускорения.
Ускорение — это физическая величина. Он определяет, как быстро изменяется скорость. Как вы находите ускорение? Формула приведена ниже:
То есть, величина a является производной скорости по времени. Он позволяет рассчитать так называемое общее мгновенное ускорение, то есть описывает, насколько мы ускоряемся в данный момент времени.
На практике часто важно знать не мгновенное ускорение, а некоторое среднее ускорение, с которым тело двигалось в течение определенного периода времени. Его можно рассчитать по следующей формуле:
Здесь v2 и v1 — мгновенные скорости в моменты времени t2 и t1 соответственно.
Криволинейное движение
Ускорение определяет величину изменения скорости. Последний варьируется более чем по одному параметру. Она может меняться как по направлению, так и по величине. Если тело движется по прямой, то вектор скорости сохраняет свое направление. Для такого движения полное ускорение определяется только изменением коэффициента скорости. Это называется тангенциальным или касательным ускорением.
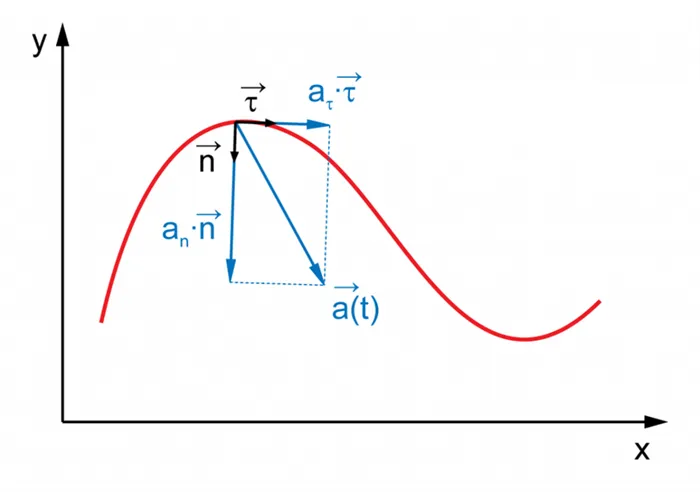
Однако если тело движется по произвольной криволинейной траектории, вектор скорости обязательно изменится. Это создает нормальную составляющую ускорения.よく見てみましょう。 Выявляя объект всех видов ускорения, вот выражение для вычисления нормального ускорения:
Это уравнение приводит к двум важным выводам:
Для определения коэффициента полного ускорения необходимо использовать следующую формулу:
Вектор a определяется как сумма векторов an и at, первый из которых направлен перпендикулярно центру кривизны, а второй — по касательной к треку в направлении изменения модуля скорости.
Свободное падение

Так называется вертикальное движение тела в гравитационном поле планеты, которое осуществляется под действием силы тяжести. Как правило, соответствующее ускорение обозначается буквой g. Например, для Земли она равна 9,81 м/с2. Приведем все формулы для ускорения g:
Первое из приведенных выше выражений позволяет определить ускорение g, если известны масса планеты M и ее радиус R; G — гравитационная постоянная. Он вытекает из закона гравитации Ньютона.
Второе выражение — это известное уравнение для гравитационной силы F, действующей на тело массой m.
Наконец, третья формула определяет ускорение через высоту падения h и время падения t тела без начальной скорости. Это выражение является одним из основных выражений в кинематике линейного движения.
Вектор тангенциального ускорения τ (см. рисунок выше) находится в том же направлении, что и линейная скорость, или противоположно ей. То есть вектор тангенциального ускорения лежит на одной оси с касательной к окружности, которая является траекторией тела.
Среднее ускорение
Среднее ускорение > — это отношение изменения скорости к периоду времени, в течение которого произошло это изменение. Среднее ускорение можно определить по формуле:

Рисунок 1.8. среднее ускорение. В СИ единицей ускорения является метр в секунду (или метр в секунду), т.е.
в квадрате в секунду равно ускорению линейно движущейся точки, скорость которой увеличивается на 1 м/с в секунду. Другими словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2 , это означает, что скорость тела увеличивается на 5 м/с в секунду.
Мгновенное ускорение
Мгновенное ускорение тела в определенный момент (материальной точке) — это физическая величина, равная пределу, к которому стремится среднее ускорение, когда промежуток времени стремится к нулю. Другими словами, это ускорение, которое тело развивает за очень короткий период времени: это ускорение, которое тело развивает за очень короткий период времени.

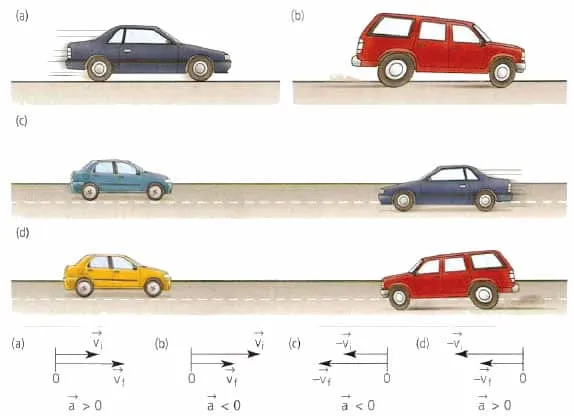
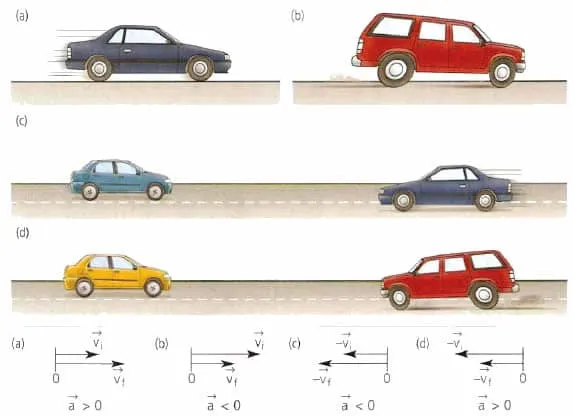
При ускоренном линейном движении скорость тела увеличивается по модулю.
Направление вектора ускорения совпадает с вектором скорости
Если скорость тела уменьшается по модулю, т.е.
Направление вектора ускорения противоположно направлению вектора скорости. Другими словами, в данном случае движение замедляется, а ускорение отрицательное (< 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рисунок 1.9. мгновенное ускорение.
Движение по криволинейной траектории изменяет не только модуль скорости, но и ее направление. В этом случае вектор ускорения представляется в виде двух компонент (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение — это составляющая вектора ускорения, направленная в определенную точку траектории при ее контакте с дорожкой. Тангенциальное ускорение характеризует изменение модулей скорости при криволинейном движении.
Рисунок 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. Другими словами, вектор тангенциального ускорения находится на той же оси, что и тангенциальная окружность, которая является траекторией движения тела.
Перемещения — это векторы, соединяющие начальное и конечное положения тела. Чтобы найти перемещение по графику скорости, нужно взять площадь над осью времени со знаком «+» и под осью со знаком «-«.
Перемещение и путь
Тело переместилось из точки А в точку Б. Перемещение тела — это отрезок, который непосредственно соединяет эти точки (векторные величины). Путь, пройденный телом, — это длина его траектории. Очевидно, что смещение и путь не следует путать. Модуль вектора перемещения и длина пути совпадают только в случае линейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Смещение равно разности между радиус-вектором в начальный момент времени и в конечный момент. Другими словами, это увеличение радиус-вектора.
Скорость и ускорение
Средняя скорость — это векторная физическая величина, равная отношению вектора перемещения к интервалу времени, за который оно произошло
Теперь представим, что временной интервал уменьшается, уменьшается и стремится к нулю, когда становится очень коротким. В этом случае мы не можем говорить о средней скорости. Скорость мгновенна. Те, кто помнит основы математического анализа, быстро понимают, что без производных мы не можем сделать то, что можем.
Мгновенная скорость — это векторная физическая величина, равная производной по времени от радиуса вектора. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и не прямолинейно, возникает ускорение, а также скорость.
Ускорение (или мгновенное ускорение) — это векторная физическая величина, вторая производная радиус-вектора по времени и, следовательно, первая производная мгновенной скорости.
Ускорение показывает, как быстро изменяется скорость тела. В случае линейного движения направления векторов скорости и ускорения совпадают. Однако в случае криволинейного движения вектор ускорения можно разложить на две составляющие: тангенциальное ускорение и нормальное ускорение.
Тангенциальное ускорение показывает, насколько быстро изменяется скорость тела, направленная по касательной к траектории.
Нормальное ускорение, с другой стороны, показывает скорость изменения скорости в направлении. Векторы нормального и тангенциального ускорения перпендикулярны друг другу, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R — радиус окружности, по которой движется тело.
Закон равноускоренного движения
Далее рассмотрим закон равномерного ускорения, то есть движение с постоянным ускорением. Рассмотрим простейший случай, когда тело движется вдоль оси x.
Здесь x — ноль, начальная координата. v ноль — начальная скорость. Продифференцируем по времени и получим скорость.
Производная скорости по времени даст значение ускорения α, которое является константой.
При прямолинейном равномерно ускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Тангенциальное ускорение.
Тангенциальное (касательное) ускорение — это составляющая вектора ускорения, направленная по касательной к траектории в данной точке траектории. Тангенциальное ускорение описывает скорость изменения скорости при криволинейном движении.

Вектор тангенциального ускорения τ (см. рисунок выше) находится в том же направлении, что и линейная скорость, или противоположно ей. То есть вектор тангенциального ускорения лежит на одной оси с касательной к окружности, которая является траекторией тела.
Нормальное ускорение.
Нормальное ускорение — это часть вектора ускорения, направленная вдоль перпендикуляра к пути движения в данной точке траектории тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рисунок выше). Нормальное ускорение описывает скорость изменения скорости в направлении и обозначается как n。 Вектор нормального ускорения направлен вдоль радиуса кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорения по правилу сложения векторов и рассчитывается по формуле:
(Теорема Пифагора для прямоугольного параллелограмма). Используя правило сложения векторов, мы также вычислим направление суммарного ускорения:
Задача: Движения двух материальных точек задаются следующими кинематическими уравнениями: $x_1=A+Bt-Ct^2$ и $x_2=D+Et+Ft^2$, каково ускорение этих двух точек в момент, когда их скорости равны, если $A$, B,C,D,E,F — константы, большие нуля.
Графики равноускоренного движения
Математически зависимость координаты от времени при изоускоренном движении является квадратичной функцией, а ее график — параболой.
Обратите внимание, что когда проекция скорости меняет знак, автомобиль поворачивает и движется в противоположном направлении.
Вся наша жизнь проходит в движении, и наши онлайн-курсы физики в Skysmart помогут вам ускорить свой путь к освоению теории и решению разнообразных задач!
Где S — расстояние, пройденное за время t м, V0— Это начальная скорость в м/с, a — ускорение тела в м/с 2 и t — время с.
Действие на людей
Часто используется термин «сила G», но G — это мера ускорения, а не мощности. Людей особенно беспокоят обычные последствия этого явления. Чтобы понять это, лучше всего обратиться к примерам.



- Все знают о поездах в парках развлечений. Скорость очень важна. Если это единственная цель дизайнера эмоционального аттракциона, то аттракцион окажется очень захватывающим. Однако все они очень умеренные, и на многих горках скорость редко превышает 30 м/с (примерно 97 км/ч). Вопреки распространенному мнению, ускорение делает вождение интересным. С помощью тщательно продуманных горок пассажиры могут на короткое время разогнаться до 3 — 4 g (при одинаковом ускорении и одинаковом замедлении). Это создает ощущение опасности на пути.
- Несмотря на огромную мощность двигателей, ускорение космического аппарата поддерживается на уровне менее 3 g. Это как то, что будет больше напрягать астронавтов и сам космический корабль. После выхода на орбиту вся система переходит в длительный период свободного падения, создавая ощущение отсутствия гравитации. Такие ощущения можно также имитировать в специально пилотируемых самолетах или на башнях свободного падения.
- Пилоты истребителей могут испытывать кратковременные ускорения до 8 g во время обычных маневров. Если удар длится более нескольких секунд, то 4-6 г достаточно, чтобы вызвать ощущения. Чтобы избежать подобных ситуаций, пилоты истребителей носят специальную одежду, которая сдавливает ноги и живот, вызывая нарушение кровоснабжения головы.
- Пилоты и космонавты также могут тренироваться со специальными центробежными емкостями, которые могут производить до 15 g. Последствия такого сильного ускорения немедленно объясняются соображениями безопасности.
- Поскольку ускорение является травмирующим фактором, наиболее распространенным датчиком конкурирующего теста является акселерометр. Экстремальное ускорение может привести к смерти.
По оценкам экспертов, ускорение во время конфликта, в котором погибла принцесса Диана, составляло 70-100 g.
Этого было достаточно, чтобы отрезать легочную артерию от ее сердца, вызвав повреждения, которые практически невозможно было пережить. Если бы Диана была пристегнута ремнем безопасности, ускорение составило бы примерно 30 или 35 g. Это грозило некоторыми переломами, но все бы выжили.