Космические скорости (приставка 1-4) — это скорости, при которых происходит качественное изменение движения космических объектов в гравитационных полях небесных тел и их систем.
Виды космических скоростей и чему они равны
Когда предмет подбрасывается вверх, он через некоторое время возвращается на поверхность Земли. Даже спутник, запущенный в космос полвека назад, космическая станция или Луна движутся в определенном направлении по орбите, как будто на них не влияет гравитационное притяжение нашей планеты.
Этому явлению есть научное объяснение. Следовательно, на Земле должна существовать гравитационная сила, сила, которая может противодействовать гравитации. Эта сила называется центробежной силой.
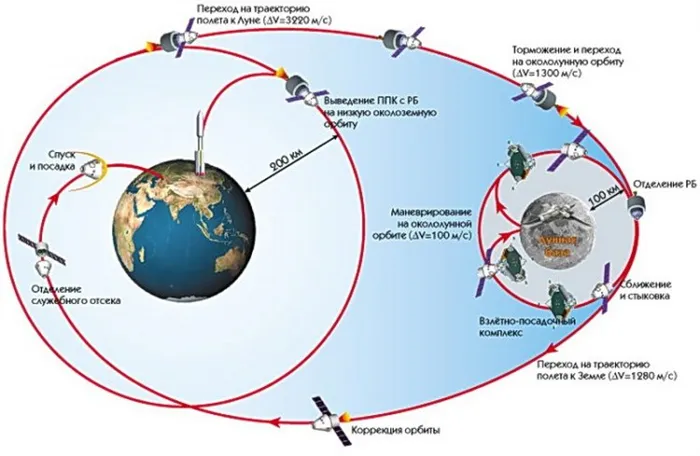
Вы можете почувствовать центробежную силу, если прикрепите один конец нити к небольшому грузику и раскрутите его по кругу. При увеличении скорости вращения натяжение нити увеличивается. Если скорость вращения замедляется, вес с большей вероятностью упадет на землю. На рисунке показана орбита космического зонда:
Внимание! Если учитель обнаружит плагиат в вашей работе, вам не избежать значительных проблем (вплоть до исключения из школы). Если вы не можете написать работу самостоятельно, закажите ее здесь.
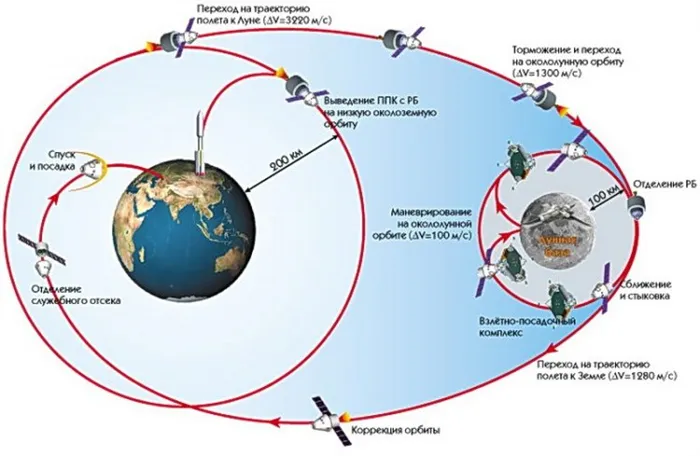
На основе рассмотренных выше примеров можно представить формулировку понятия «космическая скорость». В упрощенном виде понятие «космическая скорость» — это скорость, с которой объект может преодолеть гравитацию небесного тела и его системы.
Космические скорости (первая v1, вторая v2, третья v3 и четвертая v4) — это характерные критические скорости, с которыми космические объекты движутся в гравитационных полях небесных тел и их систем.
Космические скорости используются для характеристики типов движения космических аппаратов в сфере влияния небесных тел:
- Солнце;
- Земля;
- Луна;
- другие планеты и их естественные спутники;
- астероиды и кометы.
Все объекты, движущиеся по орбите, имеют космическую скорость. В то же время космические объекты характеризуются определенными размерами и формой орбит, которые зависят от величины и направления скорости, которую получает объект при выключении двигателей, а также от высоты, на которой происходит это выключение.
Сколько скоростей в астрономии, в чем измеряются
С древних времен исследователи наблюдали, что планеты движутся по очень сложным орбитам вокруг звезд по сравнению со звездами, которые сохраняют свое относительное положение в пространстве на протяжении веков. Древнегреческий ученый К. Птолемей дал объяснение круговому движению планет во втором веке нашей эры.
Он предположил, что Земля находится в центре Вселенной и что каждая из планет движется по маленькому кругу (эпициклу). Центр эпицикла, в свою очередь, равномерно движется по большому кругу, в центре которого находится Земля. Эта концептуальная теория получила название птолемеевской или геоцентрической системы мира.
В начале XVI века польский астроном Н. Коперник (1473-1543) создал гелиоцентрическую систему. Согласно этой концепции, небесные тела движутся благодаря движению Земли и других планет вокруг Солнца и ежедневному вращению нашей планеты.
В то время теория наблюдения Коперника воспринималась обществом как забавная фантазия. В 16 веке церковь представила это утверждение как ересь. Согласно известным фактам, З. Бруно, открыто поддержавший гелиоцентрическую систему Коперника, был предан суду и приговорен к казни на костре.
Несмотря на отсутствие поддержки в широких кругах, геоцентрическая система мира в конечном итоге была принята научным сообществом. Это было в начале 17 века, когда большинство ученых уже собрали доказательства в пользу этой теории. Иоганн Кеплер вывел из результатов многочисленных наблюдений Тихо Браге законы, которым подчиняются движения планет вокруг Солнца.
Иоганн Кеплер (1571 — 1630) был немецким ученым и одним из основателей небесной механики. Он много работал в области астрономии, механики и математики. Используя наблюдения Тихо Браге и собственные исследования, ученый открыл законы движения планет, известные как три закона Кеплера. Кеплер также известен как разработчик телескопа «Кеплер», который состоит из пары биконвексных линз.
Ньютон открыл закон всемирного тяготения, основанный на трех законах Кеплера.
Первый закон Кеплера: все планеты движутся по эллипсоидам с Солнцем в одном из их центров.
Второй закон Кеплера: радиус-вектор планеты описывает равные площади в равные моменты времени.
Третий закон Кеплера: квадраты орбитальных периодов планет относятся к кубам полуосей их орбит.
Все планеты, кроме Плутона, имеют почти круговые орбиты. В этом случае автоматически действуют первый и второй законы Кеплера. Согласно третьему закону:
Где T — период орбиты,
R — радиус орбиты.
Ньютону удалось решить обратную задачу механики, и с помощью законов планетарного движения он пришел к формуле, выражающей силу тяготения:
Согласно тому, что известно, гравитационные силы являются консервативными силами. Когда тело движется в гравитационном поле консервативных сил по замкнутому пути, работа равна нулю. Из-за консервативной природы гравитационных сил было введено понятие потенциальной энергии. Таким образом, потенциальная энергия тела массы m, удаляющегося от большого объекта массы M на расстояние r, равна:
В данном случае знак минус означает, что гравитационные силы являются притягивающими силами. Если тело находится в гравитационном поле, удаляется от центра тяжести на определенное расстояние r и имеет определенную скорость v, то его полная механическая энергия рассчитывается по формуле:
Виды космических скоростей
Одним из первых, кто ввел понятие космических скоростей и метод определения их значений, был русский ученый, который считается одним из пионеров современных космических путешествий, Ари Абрамович Штернфельд. Термин «космическая скорость» был открыт им в книге «Введение в космонавтику» в 1934 году.
Космическая скорость — это минимальная скорость, достаточная для свободного движения тела:
- v1 — играть роль спутника небесного тела, то есть приобрести способность вращаться по орбите около небесного тела и не достигать его поверхности;
- v2 — преодолеть гравитационное притяжение небесного тела и начать движение по орбите в виде параболы;
- v3 — выйти в процессе запуска за пределы планеты, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы выйти за пределы Галактики.
Космические скорости могут быть рассчитаны на любом расстоянии от центра Земли. В космической науке обычно используются значения, определенные специально для поверхности сферической однородной модели Земли с радиусом 6371 км.
Первая скорость
Первая космическая скорость (LOS v1) — это скорость, необходимая для выведения неподвижного объекта на круговую орбиту с радиусом, равным радиусу планеты, пренебрегая атмосферным сопротивлением и вращением планеты. В случае Земли значение первой космической скорости составляет 7,9 км/с.
Поэтому первая космическая скорость — это минимальная скорость, при которой тело движется горизонтально над поверхностью планеты и не падает на нее, а продолжает двигаться по круговой орбите. Чтобы определить первую космическую скорость, необходимо рассмотреть равенство между центробежной силой и гравитационной силой, действующей на тело на круговой орбите:
Здесь m — масса объекта,
M — масса планеты,
G — гравитационная постоянная,
\(v_\) — первая космическая скорость.
Если подставить числовые значения (для Земли M = 5,97-1024 кг, R = 6,378 км), то получится первая космическая скорость:
Первая космическая скорость может быть рассчитана с помощью ускорения, обусловленного гравитацией:
Вторая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — это наименьшая скорость, необходимая объекту (например, космическому кораблю) с ничтожно малой массой по сравнению с массой небесного тела (например, планеты) для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что тело, развивающее вторую космическую скорость, не испытывает негравитационного ускорения. В этом случае двигатель должен быть выключен, а атмосфера должна отсутствовать.
Вторую космическую скорость можно определить, если известны радиус и масса небесного тела. Поэтому вторая космическая скорость рассчитывается специально для каждого небесного тела, т.е. для каждой планеты, и отражает ее характеристики:
- в случае Земли значение второй космической скорости составляет 11,2 км/с. Тело, двигающееся с такой скоростью вблизи нашей планеты, выходит за ее пределы и становится спутником Солнца;
- для Солнца вторая космическая скорость составляет 617,7 км/с;
- вторая космическая скорость для Луны равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.