Скорость изменения магнитных потоков в цепи определяет величину ЭДС, индуцируемой в цепи. Сама скорость Ei будет определяться по формуле:
Магнитная индукция. Определение и описание явления.
Магнитная индукция (обозначается символом В) — основная характеристика магнитного поля (векторная величина), определяющая силу воздействия на движущийся электрический заряд (ток) в магнитном поле, направленном в направлении, перпендикулярном скорости движения.
Магнитная индукция определяется способностью воздействовать на объект с помощью магнитного поля. Эта способность проявляется при движении в катушке постоянного магнита, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается.
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка изготовлена из металла). В кристаллической решетке металла имеются электрические заряды — электроны. Если на металл не действует магнитное воздействие, то заряды (электроны) покоятся и никуда не движутся.

Если металл падает под действием переменного магнитного поля (за счет движения постоянного магнита внутри катушки, то есть смещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости движения одного относительно другого.
Когда металлическую катушку помещают в магнитное поле, заряженные частицы в металлической решетке (в катушке) поворачиваются на определенный угол и выстраиваются вдоль силовых линий магнитного поля.
Чем больше сила магнитного поля, тем больше будет вращаться число частиц и тем равномернее будет их расположение.
Магнитные поля, ориентированные в одном направлении, не компенсируют друг друга, а складываются, образуя единое поле.
Чтобы найти искомую силу, действующую на квадратную рамку с током в поле длинного провода, предположим, что под действием магнитной силы рамка сместится на небольшое расстояние dx. Это означает, что сила совершает работу, равную:
Зависимости магнитного потока
Используя формулу, видно, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Следовательно, большая площадь означает большой поток, а маленькая площадь означает малый магнитный поток.
Если, с другой стороны, магнитное поле В увеличится, то увеличится и магнитный поток. Сильное магнитное поле приводит к большому магнитному потоку, слабое поле — к маленькому магнитному потоку.
В общем, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α несколько сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, поэтому ваш угол равен α = 0°. Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, то магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого она снова начинает увеличиваться.
Примеры
Приведенные ниже примеры помогут вам лучше понять, что такое новая концепция и аналогия с текущей водой.
2. А в каком случае при ненулевой магнитной индукции ФВ = 0 ?
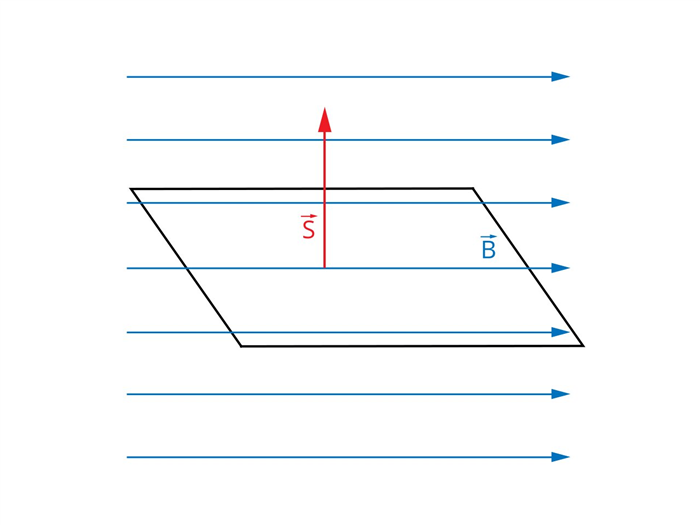
Рис. 3. Поверхность параллельна силовым линиям магнитного поля. Векторы B и S перпендикулярны
Определение магнитного потока показывает, что это имеет место, когда:
потому что cos 90° = 0.
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность по отношению к векторам магнитной индукции.
Обратите внимание, что FB можно представить как произведение B и S⟂, где S⟂ = S * cos α. Аналогичным образом всегда можно вычислить величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на площадь поверхности (см рис. 4а и 4б.).
Рис. 4а. Поверхность S⊥ является проекцией поверхности S в направлении, параллельном силовым линиям магнитного поля. 4б. Вектор B⟂ является проекцией вектора B в направлении вектора S
Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы разделим поверхность, через которую мы должны вычислить поток, на области настолько малые, что мы можем считать их плоскими, а поле — однородным. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается как:
Вычислять такие интегралы совершенно не обязательно, но полезно понимать смысл такой процедуры.
Когда металлическую катушку помещают в магнитное поле, заряженные частицы в металлической решетке (в катушке) поворачиваются на определенный угол и выстраиваются вдоль силовых линий магнитного поля.
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δA сил магнитного поля выражается через элементарное изменение потока вектора магнитной индукции dΦ :
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равна:
A = I Φ 2 — Φ 1 , где Φ 1 — поток через контур в начале движения, а Φ 2 — поток через контур в конце движения.
Теорема Гаусса для магнитного поля
Величина полного магнитного потока через замкнутую поверхность S равна нулю:
Выражение ∮ B → d S → = 0 справедливо для любого магнитного поля. Это уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
Обозначение ∮ B → dS → = 0 указывает на то, что источником магнитного поля являются не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током I, возле которого находится квадратная рамка. Через него проходит ток с силой I’. Сторона рамы представляет собой . Он расположен в одной плоскости с кабелем, как показано на рисунке 2. Величина расстояния от ближайшей стороны каркаса до проводника равна b. Найти работу, совершаемую магнитной силой при удалении рамки из поля. Рассмотрим постоянные токи.
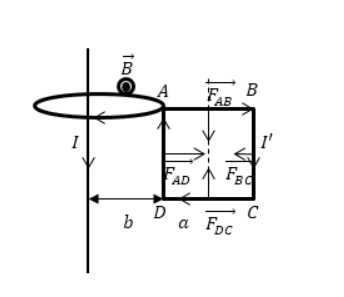
Индукция магнитного поля длинного проводника с током в той части, где расположена квадратная рамка, направлена на нас.
Следует отметить, что токовая петля находится в неоднородном поле, а это означает, что магнитная индукция уменьшается по мере удаления от провода.
Возьмем за основу формулу магнитного потока и работы, которая их объединяет:
А = I’ Φ 2 — Φ 1 (1 . 1) , где I’ принята за интенсивность тока в рамке, Φ 1 — за поток через квадратную рамку на расстоянии от ее стороны до кабеля равно B. Φ2 = 0 . Это связано с тем, что конечное положение кадра находится вне магнитного поля, как указано в условии. Отсюда следует, что запись формулы (1.1) изменится:
Перейдем к нормали n → и выберем ее направление к контуру квадрата относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченных границей квадратной рамки, угол между нормалью n → и вектором B → равен π. Записав формулу потока через поверхность рамки на расстоянии х от провода, примет вид:
d Φ = — B d S = — B a dx = — µ 0 2 π I ldxx (1 . 3) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет равно:
Отсюда следует, что для нахождения полного потока (1.3) потребуется:
Φ 1 = ∫ S — μ 0 2 π i ldxx = — μ 0 2 π i l ∫ bb + adxx = — μ 0 2 π i l at b + ab (1 . 5) .
Подставим формулу (1.5) в (1.2). Требуемая работа равна:
А знак равно я ‘ μ 0 2 π я л пер б + аб .
Ответ: A = μ 0 2 π II ‘ l · ln b + ab .
Найдите силу, действующую на раму в предыдущем примере.
Чтобы найти искомую силу, действующую на квадратную рамку с током в поле длинного провода, предположим, что под действием магнитной силы рамка сместится на небольшое расстояние dx. Это означает, что сила совершает работу, равную:
Элементарную работу δA можно выразить как:
Сделаем то же самое сильно, применяя формулы (2.1), (2.2). Мы получаем:
F dx знак равно я ‘ d Φ → F знак равно я ‘ d Φ dx (2 . 3) .
Воспользуемся выражением, полученным в примере 1 :
d Φ знак равно — μ 0 2 π я ldxx → d Φ dx знак равно — μ 0 2 π я lx (2 . 4) .
Сделаем замену d Ф dx в (2.3) . У нас есть:
F знак равно я ‘ μ 0 2 π я лкс (2 . 5) .
Каждый элемент контура квадратной рамки находится под действием сил (силы Ампера). Отсюда следует, что на раму действуют четыре силы, причем стороны AB и DC равны по абсолютной величине и противоположны по направлению. Выражение принимает вид:
Расход является скалярной величиной и его единицей является вебер (Вб): 1 Вб = 1 Тл * м 2 , то есть F = Т * м 2 . Магнитный поток обозначается как Ф (символом формулы является греческое фи).
Теорема Гаусса для магнитной индукции
Великий немецкий ученый Карл Гаусс, преуспевающий в математике, физике и астрономии, вывел закон (теорему) в области магнетизма. Он показал, что в отличие от электрического поля, создаваемого электрическими зарядами, МП не создается магнитными зарядами. Их просто не существует в классической электродинамике.
Информация Теорема, которую вывел Гаусс, относится к основным законам электродинамики и является частью системы уравнений Максвелла. Он описывает связь между потоком силы электрического поля, пронизывающей произвольную замкнутую поверхность, и суммой зарядов, помещенных в объем, ограниченный этой поверхностью. Сумма выражается алгебраически.
По отношению к магнитной индукции поток B→, проходящий через замкнутую поверхность S, имеет нулевое значение.
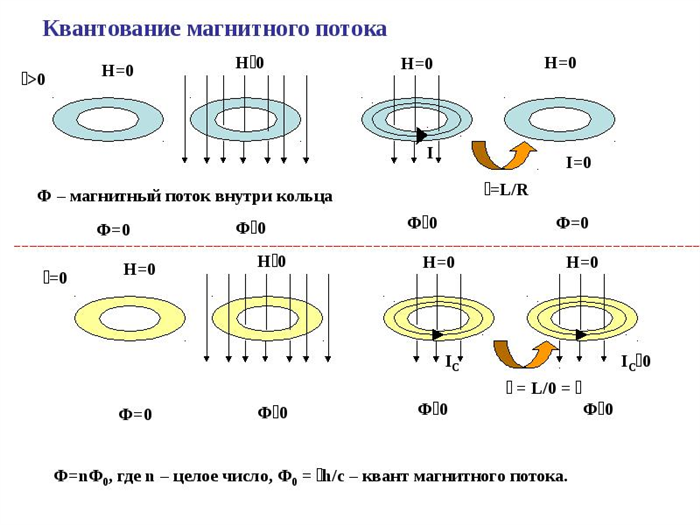
Квантование магнитного потока
В 1961 г практически было установлено, что если через замкнутый сверхпроводник, по которому течет электричество, направить магнитный поток, то величина Ф будет кратна кванту потока Ф0 = h/2e = 2,067833758·10-15Wb. Это значение ДА.
Такой эксперимент провели американцы Дивер и Фэрбэнк. Они выполнили количественную оценку с помощью трубки полой конструкции, пропуская через нее круговые токи сверхпроводящего характера. В результате его квантовая размерность оказалась в два раза меньше. Это было связано с тем, что электроны в сверхпроводящей ситуации разделялись на пары. Частицы образовывали пары с зарядом 2e. Именно движение этих пар и составляет природу сверхпроводящего тока.
Довожу до вашего сведения. Сверхпроводники — это материалы, у которых при снижении температуры до определенного значения сопротивление резко падает. Он практически равен нулю, поэтому можно говорить о сверхпроводящих свойствах. Металлы, являющиеся прекрасными проводниками (золото, серебро, платина), не приобретают в таких условиях сверхпроводящих способностей.
Если, с другой стороны, магнитное поле В увеличится, то увеличится и магнитный поток. Сильное магнитное поле приводит к большому магнитному потоку, слабое поле — к маленькому магнитному потоку.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении пронизывающего его магнитного потока.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел серию экспериментов, которые помогли открыть явление электромагнитной индукции.
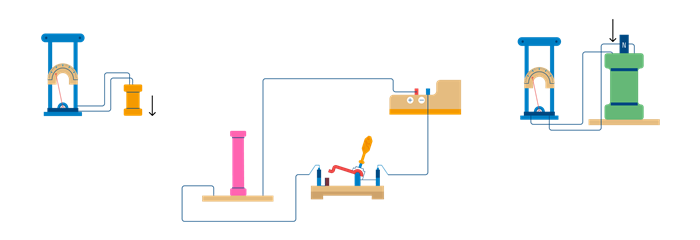
Опыт раз. На непроводящем основании были намотаны две катушки: витки первой катушки располагались между витками второй. Витки одной катушки замыкались в гальванометре, а вторая подключалась к источнику тока.
При закрытии крана и протекании тока через вторую катушку в первой возникал импульс тока. При открытии крана также наблюдался импульс тока, но ток через гальванометр протекал в обратном направлении.
Опыт два. Первая катушка была подключена к источнику тока, а вторая к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки регистрировался ток.
Опыт третий. Катушка замкнута на гальванометр и магнит перемещается внутрь (вне) относительно катушки
Вот что показали эти эксперименты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет разным и при увеличении числа линий, и при его уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Само поле может меняться, или контур может двигаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток может существовать в цепи, когда внешние силы действуют на свободные заряды. Работа, совершаемая этими силами при перемещении одиночного положительного заряда по замкнутому контуру, равна ЭДС.
Это означает, что при изменении числа магнитных линий поперек поверхности, ограниченной контуром, на ней возникает ЭДС, называемая ЭДС индукции.
Онлайн-курсы физики Skysmart так же интересны, как и наши статьи!
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически это можно описать формулой:
Закон Фарадея
ΔF/Δt – скорость изменения магнитного потока, Втб/с
Знак «-» в формуле позволяет учитывать направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, создаваемого этим током, через поверхность, ограниченную контуром, уменьшал изменения поля, вызвавшие появление индукционного тока.
Если цепь состоит из N витков (т.е это катушка), то ЭДС индукции будет рассчитываться следующим образом.
Закон Фарадея для цепи из N витков
ΔF/Δt – скорость изменения магнитного потока, Втб/с
Сила индукционного тока в замкнутой проводящей цепи сопротивлением R:
Закон Ома для проводящей цепи
I — сила индукционного тока А
R — сопротивление цепи Ом
Если проводник длиной l движется со скоростью v в постоянном однородном магнитном поле с индукцией B, то ЭДС электромагнитной индукции равна:
Индукционный МКЭ для движущегося проводника
v — скорость водителя м/с
Возникновение ЭДС индукции в проводнике, движущемся в магнитном поле, объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца в этом случае играет роль внешней силы.
Проводник, движущийся в магнитном поле, по которому течет индукционный ток, испытывает магнитное торможение. Суммарная работа силы Лоренца равна нулю.
Количество теплоты в цепи выделяется за счет работы внешней силы, поддерживающей постоянной скорость проводника, или за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- за счет движения контура или его частей в постоянном магнитном поле во времени. Это тот случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- за счет изменения во времени магнитного поля при неподвижном контуре. В этом случае появление ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, индукционные явления в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Майкл Фарадей открыл явление, известное как электромагнитная индукция. В 1831 г было замечено, что если магнитный поток Ф, пронизывающий цепь, состоящую из замкнутого проводника, изменяется, то в ней индуцируется электрический ток.
Электрическая зависимость

Английский физик Майкл Фарадей в своей теореме не сомневался в уникальности явлений магнетизма. Изменяющийся во времени фон создает электронный и магнетический вид. В 1831 году Фарадей обнаружил появление индукции, которая легла в основу устройства генераторов, преобразующих механическую энергию в электронную. А в 1835 году немецкий математик Карл Гаусс сформулировал аксиому, описывающую назначение и зависимость напряженности поля от величины заряда.
Появление электрической индукции отмечается в появлении тока в проводящей цепи, который либо стоит на изменяющемся во времени фоне, либо движется в неизменном сечении таким образом, что фактически число магнитных витков проникает контуры преобразований.
Для своих многочисленных экспериментов Фарадей использовал две катушки, магнит, переключатель постоянного тока и гальванометр. Поток электронов может зависеть от куска железа и намагничивать его.
В результате опытов Фарадея были установлены основные черты возникновения электрической индукции и появления тока:
- в одной из катушек при замыкании или размыкании электронной цепи внутри другой части;
- при перетекании мощности в один из элементов, поддерживаемых реостатом;
- при перемещении катушек относительно друг друга;
- когда постоянный магнит движется относительно.
В замкнутом проводящем контуре ток возникает при изменении числа линий магнитной индукции, создающих плоскость, ограниченную контуром. И чем раньше будет перенесено количество рядов МИ, тем больше будет индукционный ток в раме. Это основная причина изменения количества индукционных последовательностей.
Явление позволяет содержать и изменять количество линий МИ, делая план участка ограниченным фиксированной проводящей цепью, за счет конфигурации тока в расположенной рядом катушке. Наблюдается максимальное изменение количества последовательностей ИМ за счет смещения схемы на неоднородном фоне, плотность линий которого может меняться на месте.
А = I’ Φ 2 — Φ 1 (1 . 1) , где I’ принята за интенсивность тока в рамке, Φ 1 — за поток через квадратную рамку на расстоянии от ее стороны до кабеля равно B. Φ2 = 0 . Это связано с тем, что конечное положение кадра находится вне магнитного поля, как указано в условии. Отсюда следует, что запись формулы (1.1) изменится:
Проводящая рамка в магнитном поле
Явление электромагнитной индукции заключается в том, что при изменении поля, проникающего в проводящий каркас или катушку, возникает электродвижущая сила (ЭДС):

Рис. 1. Электромагнитная индукция, опыт Фарадея.
Энергия магнитного поля, используемая в этом эксперименте, характеризуется магнитной индукцией. Однако при попытке описать наблюдаемое явление оказалось, что одного этого количества недостаточно.
Если записать в таблицу значения ЭДС, индуцируемые магнитным полем, имеющим одинаковую плотность магнитных линий при разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, гораздо важнее, чем ЭДС в длинной узкой рамке. (с периметром).
Причиной тому был разный «полевой охват» кадра. Площадь длинного узкого кадра мала, он «закрывает» небольшое «количество поля», и ЭДС тоже мала. Квадратная рамка имеет большую площадь при том же периметре, а круглая катушка имеет наибольшую площадь, в результате рамка «покрывает» большее «количество поля», и ЭДС в такой рамке тоже оказывается больше большой
Не менее важной была ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям, то независимо от ее площади и силы магнитного поля в рамке не будет создаваться ЭДС.
Понятие магнитного потока
Так, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. Это понятие объединяет все величины, от которых зависит ЭДС индукции в рамке: индукция поля, площадь и ориентация рамки. Для обозначения используется заглавная греческая буква Ф (phi):
Таким образом, магнитный поток есть величина, равная произведению индукции магнитного поля, площади проводящего контура и косинуса угла между нормалью к контуру и направлением линий индукции.
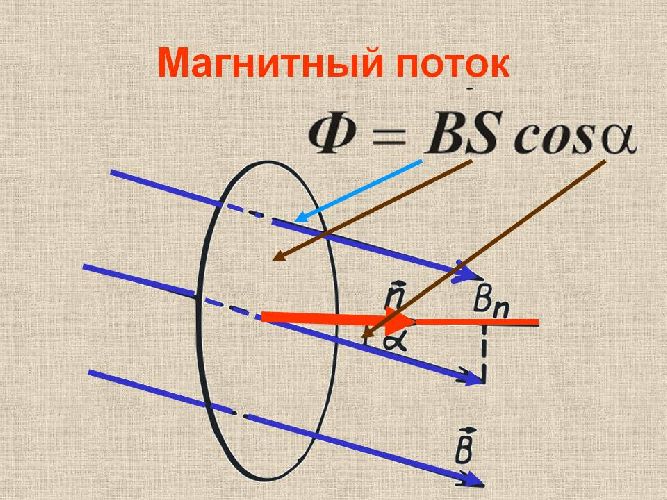
Рис. 2. Магнитный поток Ф=Вшт.
Из приведенной выше формулы для магнитного потока можно вывести определение его единицы — Вебера (Вб):
то есть 1 магнитный поток Вебера — это магнитный поток через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1 Тесла.

Рис. 3. Магнитный поток зависит от…
Чтобы понять термин «магнитный поток», можно провести аналогию с обычным течением воды. Расход воды, как правило, зависит от напора воды (аналог индукции) и площади поперечного сечения трубы (аналог площади рамы), а так как вода, в отличие от магнитного поля, он всегда заключен внутри трубы, поток воды всегда ориентирован вдоль сечения трубы, а значение косинуса в формуле всегда равно единице.