6. Пружина жесткостью 200 Н/м растянута на 5 см. Какую работу совершит сила упругости, когда пружина вернется в равновесие?
Новости и знаменательные даты
Механическая работа и мощность. Единицы измерения работы и мощности.
Короткий ответ
Механическая работа — это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и косинус угла между вектором силы и вектором перемещения (или скорости).
F — Сила, действующая на тело
S — перемещение, которое совершает тело под действием силы
a — угол между направлением силы и вектором смещения
В системе СИ работа измеряется в джоулях (Дж).
1Дж=1Нм
Работа, совершаемая силой в единицу времени, называется мощностью.
Мощность N — физическая величина, равная отношению работы A к интервалу времени t, в течение которого эта работа совершается:
В Международной системе (СИ) единицей мощности является ватт (Вт).
Блок питания вне системы 1 л.с.=735 Вт
Подробный ответ
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело движется под действием этой силы, то говорят, что сила совершает работу.

Механическая работа — это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и косинус угла между вектором силы и вектором перемещения (или скорости).
F — Сила, действующая на тело
S — перемещение, которое совершает тело под действием силы
a — угол между направлением силы и вектором смещения
В системе СИ работа измеряется в джоулях (Дж). Один джоуль равен работе, совершаемой силой 1 Н при перемещении на 1 м в направлении действия силы.
1Дж=1Нм
1) Если направление силы совпадает с направлением движения тела, т е. α = 0, cos α = 1, то
2) Если сила направлена перпендикулярно направлению движения тела, то есть α = 90º, cos α = 0, то
Следовательно, если тело движется в направлении, перпендикулярном направлению действия силы, то сила не совершает работы.
3) Если угол между направлением силы и направлением движения тупой, т.е. α > 90º, cos α < 0, то
4) Если движение происходит в направлении, противоположном направлению вектора силы, то есть α = 180 º, cos α = -1, то
Например, работа силы сопротивления отрицательна.
Графически работа определяется площадью криволинейной фигуры под графиком Fs(x)

Работа, совершаемая силой в единицу времени, называется мощностью .
Мощность N — физическая величина, равная отношению работы A к интервалу времени t, в течение которого эта работа совершается:
В Международной системе (СИ) единицей мощности является ватт (Вт). Один ватт равен мощности силы, которая совершает работу в 1 Дж за 1 секунду.
Блок питания вне системы 1 л.с.=735 Вт
Зависимость между мощностью и скоростью при равномерном движении:
N=A/t, поскольку A=FScosα, тогда N=(FScosα)/t, но S/t = v, поэтому
N=Fvcosα
Какую работу совершает сила упругости, когда пружина жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, внешние силы на пружину не действуют.
Механическая работа. Мощность

1. Механическая работа \(A\) — это физическая величина, равная произведению вектора силы, действующей на тело, на вектор его перемещения: \(A=\vec \vec \) . Работа есть скалярная величина, характеризуемая числовым значением и единицей.
Единицей работы является 1 джоуль (1 Дж). Это работа силы 1 Н на пути 1 м.
2. Если сила, действующая на тело, составляет с перемещением некоторый угол \(\alpha\) , то проекция силы \(F\) на ось X равна \(F_x \) (рис. 42).
Так как \(F_x=F\cdot\cos\alpha \) , то \(A=FS\cos\alpha \) .
Таким образом, работа постоянной силы равна произведению модулей векторов силы и смещения на косинус угла между этими векторами.
3. Если сила \(F\) = 0 или перемещение \(S \) = 0, то механическая работа равна нулю \(A \) = 0. Работа равна нулю, если вектор силы перпендикулярна вектору перемещения, т е сила перпендикулярна направлению движения тела в любой точке пути.
4. Работа силы может быть как положительной, так и отрицательной. Работа положительна \(A \) > 0, если угол равен 90° > \(\alpha \) ≥ 0°; если угол 180° > \(\alpha \) ≥ 90°, то работа отрицательна \(A \) < 0.
Если угол \(\alpha \) = 0°, то \(\cos\alpha \) = 1, \(A=FS \) . Если угол \(\alpha \) = 180°, то \(\cos\alpha \) = -1, \(A=-FS \) .
5. При свободном падении с высоты \(h\) тело массой \(m\) перемещается из положения 1 в положение 2 (рис. 43). В этом случае сила тяжести совершает работу, равную:
Когда тело движется вертикально вниз, сила и перемещение направлены в одном направлении, и сила тяжести совершает положительную работу.
Если тело поднимается, то сила тяжести направлена вниз, а двигаясь вверх, сила тяжести совершает отрицательную работу, т.е.
6. Работу можно представить графически. На рисунке изображен график зависимости силы тяжести от высоты тела относительно поверхности Земли (рис. 44). Графически работа силы тяжести равна площади фигуры (прямоугольника), ограниченной графиком, осями координат и перпендикуляром, проведенным к оси абсцисс
в точке \(h \) .
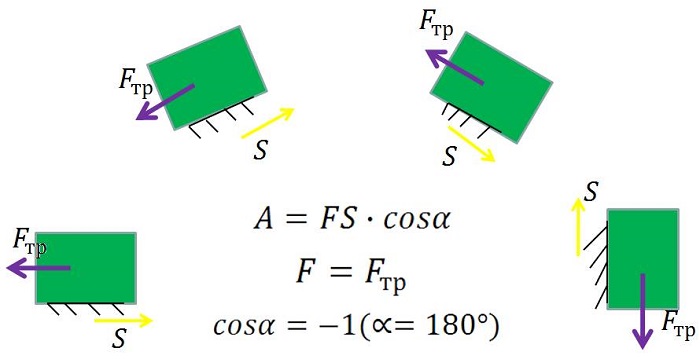
График зависимости силы упругости от удлинения пружины представляет собой прямую линию, проходящую через начало координат (рис. 45). По аналогии с работой силы тяжести работа силы упругости равна площади треугольника, ограниченного графиком, осями координат и перпендикуляром, проведенным к оси абсцисс в точке \(х \) .
\(A=Fx/2=kx\cdot x/2 \) .

7. Работа силы тяжести не зависит от формы пути, по которому движется тело; Это зависит от начального и конечного положения тела. Пусть сначала тело переместится из точки А в точку В по пути АВ (рис. 46). Работа силы тяжести в этом случае
ПРИМЕРЫ ЗАДАНИЙ
1. Работа определяется по формуле
1) \(А=Fv \)
2) \(А=N/t \)
3) \(А=мв \)
4) \(А=ПС \)
2. Груз поднимают равномерно вертикально вверх за привязанную к нему веревку. Работа силы тяжести в этом случае
1) равный нулю
2) положительный
3) отрицательный
4) Повышение эластичности рабочей силы
3. Ящик тянут за привязанный к нему канат, образуя с горизонтом угол 60°, приложив силу 30 Н. Какова работа этой силы, если модуль смещения равен 10 м?
1) 300Дж
2) 150 Дж
3) 3Дж
4) 1,5 Дж
4. Искусственный спутник Земли, масса которого равна \(m\) , движется равномерно по круговой орбите радиусом \(R\) . Работа, совершаемая силой тяжести за время, равное периоду обращения, равна
1) \(мгР \)
2) \(\pimgR \)
3) \(2\pimgR \)
4) \(0 \)
5. Автомобиль массой 1,2 т проехал 800 м по ровной дороге. Какую работу совершила при этом сила трения, если коэффициент трения равен 0,1?
1) -960кДж
2) -96кДж
3) 960кДж
4) 96кДж
6. Пружина жесткостью 200 Н/м растянута на 5 см. Какую работу совершит сила упругости, когда пружина вернется в равновесие?
1) 0,25 Дж
2) 5Дж
3) 250Дж
4) 500Дж
7. Шарики одинаковой массы катятся с горки по трем разным пандусам, как показано на рисунке. В каком случае работа силы тяжести будет больше?

11
2) 2
3) 3
4) работа во всех случаях одинакова
8. Работа по замкнутому пути равна нулю
А. Силы трения
Б. Силы упругости
1) и А, и Б
2) только А
3) только Б
4) ни А, ни Б
9. Единицей мощности в СИ является
10. Чему равна полезная работа, если совершенная работа равна 1000 Дж, а КПД двигателя равен 40 %?
1) 40000Дж
2) 1000Дж
3) 400Дж
4) 25Дж
11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В своем ответе подпишите выбранные числа под соответствующими буквами.
СИЛОВАЯ РАБОТА
А. Работа силы упругости при растяжении пружины
Б. Работа силы трения
Б. Работа силы тяжести при падении тела
РАБОТА ЗНАК
1) положительный
2) отрицательный
3) равный нулю
12. Из приведенных ниже утверждений выберите два верных и запишите их номера в таблицу.
1) Работа силы тяжести не зависит от формы траектории.
2) Работа совершается при любом движении тела.
3) Работа силы трения скольжения всегда отрицательна.
4) Работа силы упругости в замкнутом контуре не равна нулю.
5) Работа силы трения не зависит от формы пути.
Для улучшения работы сайта и его взаимодействия с пользователями мы используем файлы cookie, которые хранятся на вашем компьютере. Нажимая ПРИНЯТЬ, вы подтверждаете, что знаете об использовании файлов cookie на нашем веб-сайте и разрешаете использование файлов cookie. Вы можете отключить файлы cookie в настройках вашего браузера.
Примеры решения задач
Задача 1
Ложка медленно погружается в большую банку с медом. На него действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил совершает положительную работу при движении тела? Выберите правильный ответ:
Ни одна из перечисленных сил.
Когда ложка падает, движение направлено вниз. Только сила тяжести направлена в ту же сторону, что и перемещение. Это означает, что она выполняет положительную работу.
Задача 2
Ящик тянут по земле на веревке по горизонтальной окружности длиной L = 40 м с постоянной модульной скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 Н. Чему равна работа толкающей силы за один оборот?
Поскольку ящик тянут с постоянной скоростью, его кинетическая энергия не меняется. Вся энергия, которая затрачивается на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу толкающей силы за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F движется вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, величина силы F равна 30 Н. Какую работу совершила сила F при этом перемещении в системе отсчета, связанной с наклонной плоскостью?
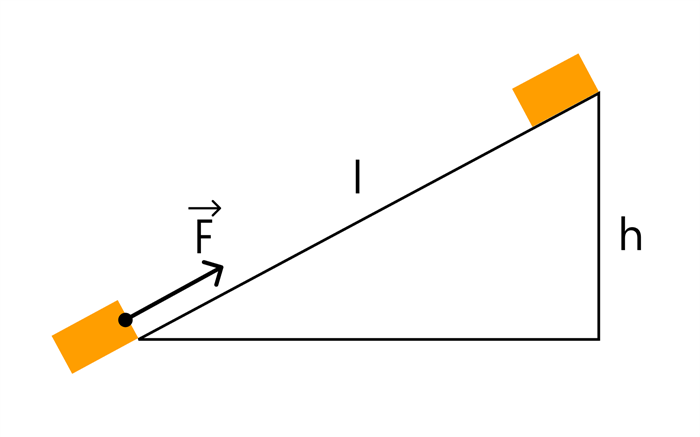
В этом случае нас просят найти работу, совершаемую силой F при перемещении тела по наклонной плоскости. Это означает, что нас интересует сила F и пройденное расстояние. Если бы нас спросили о работе силы тяжести, мы бы досчитали до силы тяжести и высоты.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Так как:
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке изображен график проекции скорости vx тела на эту ось в зависимости от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
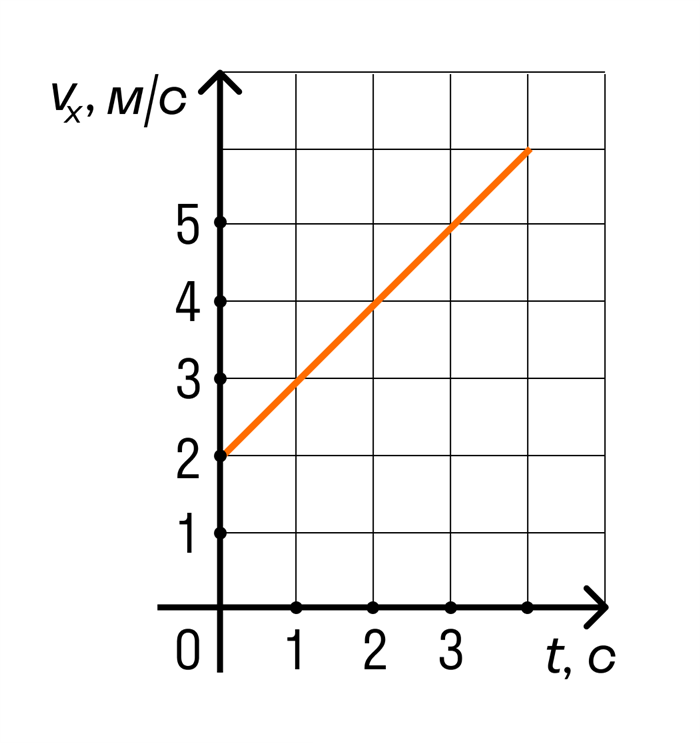
Из графика видно, что проекция скорости тела на время 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = PV = 2 × 5 = 10 Вт
Ответ: 10 Вт
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем Skysmart!
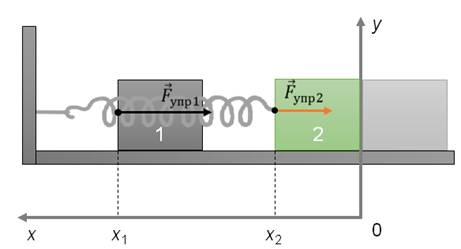
Рассмотрим систему, состоящую из пружины и тела некоторой массы, лежащего на достаточно гладкой горизонтальной поверхности. Левый конец пружины крепится к стене, а правый конец крепится к корпусу. Направим ось x, как показано на рисунке.
Потенциальная энергия
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела по отношению к поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от пути тела и определяется только начальным и конечным положениями (так называемые консервативные силы). Работа таких сил на замкнутом пути равна нулю. Этим свойством обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в гравитационном поле Земли рассчитывается по формуле:
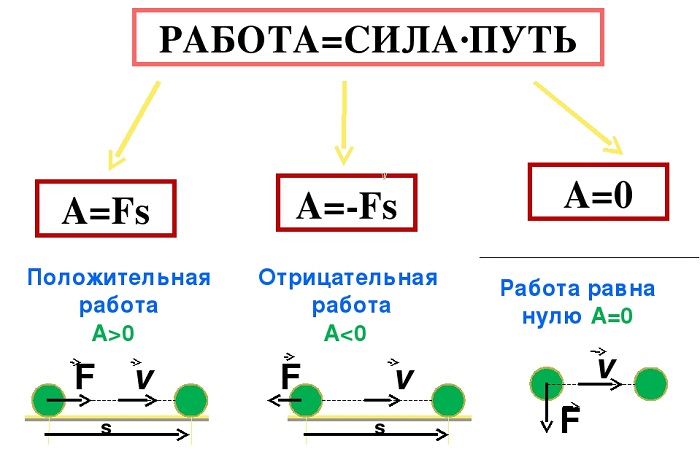
Физический смысл потенциальной энергии тела: потенциальная энергия равна работе, совершаемой силой тяжести при опускании тела на нулевой уровень (h — расстояние от центра тяжести тела до нулевого уровня уровень). Если тело обладает потенциальной энергией, то оно способно совершить работу при падении этого тела с высоты h в ноль. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с обратным знаком:

Часто в силовых задачах приходится находить работу, чтобы поднять (развернуться, выбраться из ямы) кузов. Во всех этих случаях необходимо учитывать движение не самого тела, а только его центра тяжести.
Потенциальная энергия Ep зависит от выбора нулевого уровня, т е от выбора начала оси OY. В каждой задаче для удобства выбран нулевой уровень. Физический смысл имеет не сама потенциальная энергия, а ее изменение при переходе тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Потенциальная энергия растянутой пружины рассчитывается по формуле:
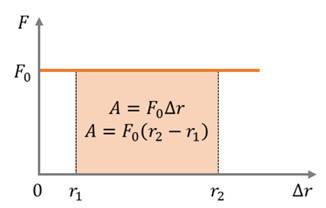
где: k – жесткость пружины. Растянутая (или сжатая) пружина способна приводить в движение прикрепленное к ней тело, то есть сообщать этому телу кинетическую энергию. Поэтому такая пружина имеет запас энергии. Растяжение или сжатие x необходимо рассчитывать из недеформированного состояния тела.
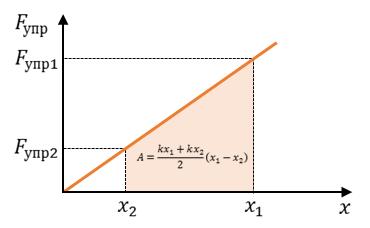
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из заданного состояния в состояние с нулевой деформацией. Если в исходном состоянии пружина уже была деформирована и ее удлинение было равно х1, то при переходе в новое состояние с удлинением х2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с обратным знаком (так как сила упругости всегда направлена против деформации тела):
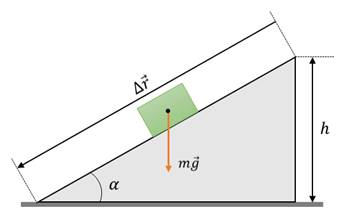
Потенциальная энергия при упругом деформировании – это энергия взаимодействия отдельных частей тела друг с другом упругими силами.
Работа силы трения зависит от пройденного пути (этот тип силы, работа которой зависит от пути и пройденного пути, называется диссипативной силой). Для силы трения нельзя ввести понятие потенциальной энергии.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — характеристика эффективности системы (устройства, машины) по отношению к преобразованию или передаче энергии. Он определяется отношением используемой полезной энергии к общему количеству энергии, полученной системой (формула уже приводилась выше).
КПД можно рассчитать как по работе, так и по мощности. Полезная и затраченная работа (мощность) всегда определяется простыми логическими рассуждениями.
В электродвигателях КПД – это отношение между совершаемой механической работой (полезной) и получаемой от источника электрической энергии. В тепловых машинах отношение полезной механической работы к количеству затраченной теплоты. В электрических трансформаторах отношение между электромагнитной энергией, полученной во вторичной обмотке, и энергией, потребляемой первичной обмоткой.
В силу своей общности понятие КПД позволяет сравнивать и оценивать с единых позиций такие разные системы, как ядерные реакторы, генераторы и электродвигатели, тепловые электростанции, полупроводниковые приборы, биологические объекты и др
Из-за неизбежных потерь энергии на трение, нагрев окружающих тел и т. КПД всегда меньше единицы. Следовательно, КПД выражается в долях затраченной энергии, т е в собственной дроби или в процентах, и является безразмерной величиной. КПД характеризует эффективность, с которой работает машина или механизм. КПД тепловых электростанций достигает 35-40%, двигателей внутреннего сгорания с наддувом и предварительным охлаждением — 40-50%, динамо-машин и генераторов большой мощности — 95%, трансформаторов — 98%.
Задача, в которой нужно найти эффективность или известна, должна начинаться с логических рассуждений: какая работа полезна, а какая тратится.
6. Пружина жесткостью 200 Н/м растянута на 5 см. Какую работу совершит сила упругости, когда пружина вернется в равновесие?
Знак работы силы
Знак работы силы однозначно определяется косинусом угла между вектором силы и вектором перемещения:
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена в сторону, противоположную движению тела (угол равен 180°). Но в геоцентрической системе отсчета работа силы трения покоя будет отлична от нуля и больше нуля, если она опирается на движущийся объект (см рисунок выше). В этом случае сила трения покоя будет направлена со смещением относительно Земли в одну сторону (угол 0°). Это происходит потому, что тело по инерции будет пытаться сохранить мир относительно Земли. Это означает, что направление возможного движения противоположно движению объекта, на котором находится это тело.
Геометрический смысл работы
Механическая работа численно равна площади фигуры, ограниченной графиком с осями ОФ и ОХ.
Мощность – это физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы А, совершаемой телом за время t:
Рассмотрим частные случаи для определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела
Работа при равномерном прямолинейном движении определяется по формуле:
Ft — сила тяги, s — перемещение тела под действием этой силы. Следовательно, мощность:
Мощность при равномерном подъеме груза
При подъеме груза совершается работа, модуль которой равен работе силы тяжести. За смещение в этом случае можно взять высоту. Потом:
Мгновенная мощность при неравномерном движении
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно рассчитать мгновенную мощность. Она равна произведению выталкивающей силы на мгновенную скорость:
Мощность силы трения при равномерном движении по горизонтали
Мощность силы трения так же, как и работа, отрицательна. Это связано с тем, что угол между векторами трения и смещения составляет 180° (косинус равен -1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения:
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. В чем твоя сила?
Коэффициент полезного действия
Не всякая работа органов может быть полезной. В реальном мире на тела действуют различные силы, препятствующие совершению работы другой силой. Например, чтобы переместить груз на определенное расстояние, нужно совершить намного больше работы, чем можно получить, вычислив по приведенным выше формулам.
- Совершенная работа — это полная работа, совершаемая силой над телом (или телом).
- Полезная работа есть часть полной работы силы, непосредственно вызывающей движение тела.
- Коэффициент полезного действия (КПД) — процент полезной работы к затраченной работе. КПД обозначается буквой «эта» — η. Эта величина не имеет единицы измерения. Показывает эффективность механизма или другой системы, выполняющей работу, в процентах.
Эффективность определяется по формуле:
Работу можно определить как произведение мощности на время, за которое была совершена работа:
Таким образом, формулу для расчета КПД можно записать следующим образом:
Частые случаи определения эффективности рассмотрим в следующей таблице:
Устройство
Работа полезная и полная
l — идеальный путь (длина наклонной плоскости).
Пример №4. Определить полезную мощность двигателя, если его КПД 40% и мощность по паспорту 100 кВт.
В этом случае нет необходимости переводить единицы измерения в СИ. Но в этом случае мы также получим ответ в кВт. Из этой формулы выразим полезную мощность:
Задача EF17557 Чему равно тяговое усилие трактора при движении прицепа со скоростью 18 км/ч, если оно равно 16,5 кН? Ответ: а) 916 Вт б) 3300 Вт в) 82500 Вт г) 297000 Вт
2. Если сила, действующая на тело, составляет с перемещением некоторый угол \(\alpha\) , то проекция силы \(F\) на ось X равна \(F_x \) (рис. 42).
Мощность
Среднее количество работы, совершаемой в единицу времени (секунду), характеризует такую величину, как мощность. Формула для его расчета выглядит так:
В качестве задания можно подставить известную формулу для своего расчета, в зависимости от ситуации. Ответ будет выражен в ваттах.
Однако при равномерном движении можно использовать другую формулу:
Подставив мгновенную скорость вместо обычной скорости, получим значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1
Какую работу совершает подъемный механизм, поднимающий 10-килограммовый блок на высоту 50 метров.
Чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимается блок, равна той, с которой притягивается к земле. Так как последний равен m*g, то для нахождения конечного результата нужна лишь модифицированная версия упомянутой выше стандартной формулы: A = S*m*g.
С помощью простой математики найдем числовой ответ:
Однако дело не всегда в гравитации.
Задача 2
Какую работу совершает сила упругости, когда пружина жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, внешние силы на пружину не действуют.
Сначала нужно найти саму эластичность F, которая выполняет работу. Его формула такова: F = x * |k|, где x — длина, на которую пружина сжимается или растягивается, а k — ее коэффициент жесткости. Перемещение пружины равно ее деформации, поэтому итоговая формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Затем с помощью элементарных вычислений вычисляем ответ:
А = (0,2 м) ^ 2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Но во всех задачах на эту тему путь тела прямой.
Задача 3
Вычислите силу, действующую на колесо, если для одного полного оборота требуется 10 кДж. Диаметр диска 40 см, толщина покрышки 10 см.
В этом случае нам нужно найти не А, а F, но это можно сделать по той же формуле. Возьмите точку на поверхности колеса. Будем считать, что при вращательном движении его вектор будет противоположен вектору приложения силы, а значит, косинусом в формуле снова можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно рассчитать как 2πr или πd. Диаметр окружности можно найти из приведенных данных: он равен сумме диаметра обода и удвоенной толщины покрышки, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 метра.
Теперь, когда мы можем рассчитать расстояние, у нас есть все данные, необходимые для определения силы.
Формула работы для этого случая будет: A = F * π * d, поэтому сила, соответственно, может быть выражена как F = A/(π * d).
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
В заключение решим самый сложный вариант задачи, включающий в себя все вышеперечисленное.
Задача 4
Автомобиль Volkswagen массой 2500 кг взбирается на гору. Какой должна быть его минимальная скорость, чтобы удержаться на горе, если тяговое усилие 10 кН, время работы двигателя 10 с, КПД 30%, а уклон горы 60 градусов? Трением и другими силами пренебречь.
На первый взгляд задача может показаться сложной, но для ее решения используются только простые и известные формулы.
Запишем условие более наглядно.
угол А = 150 0 (60 + 90, так как сила тяжести приложена под углом 90 к горизонту);
Шаг 1. По условию А1 (сила тяжести) = А2 (тяга).
Шаг 3. Общая формула: мг = F * V * cosA * t / КПД.
V = (2500кг * 10Н/кг * 30%) / (10000H * 10с * cos150);
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке изображен график проекции скорости vx тела на эту ось в зависимости от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам по набору, вам необходимо добавить его в свою учетную запись, купив его в каталоге.
Конспект урока «Механическая работа. Мощность»
Эта тема будет посвящена механической работе и мощности.
Механическая работа — скалярная физическая величина, характеризующая процесс перемещения тела под действием силы. Под действием постоянной силы тело движется прямолинейно и движется в направлении действия силы, тогда сила совершает работу, равную произведению модуля этой силы на модуль перемещения.
Из определения следует единица измерения работы в метрической системе единиц
Эта единица названа в честь английского ученого Джеймса Прескотта Джоуля, который первым экспериментально подтвердил эквивалентность работы и теплоты.
Это простейший случай, когда перемещение тела и действующая на него сила совпадают по направлению.
Теперь рассмотрим, как рассчитывается работа, когда направление силы не совпадает с направлением движения тела. Для этого рассмотрим следующий эксперимент. Через блок, на котором висит брусок определенной массы, переброшена веревка. На брусок действуют две силы: сила тяжести и сила натяжения нити.
Если за нить натянуть равномерно, то тело будет двигаться равномерно, а значит, результирующая сила, действующая на тело, будет равна нулю.
Это означает, что при некотором перемещении тела работа равнодействующей силы также будет равна нулю.
Однако натяжение нити работает.
Так как при равномерном движении величина силы натяжения нити равна силе тяжести тела, то можно считать, что сила тяжести совершает ту же по величине работу, но отрицательную.
Отсюда можно сделать вывод: работа силы может быть положительной, отрицательной или равной нулю.
Обратите внимание, что сила тяжести по направлению противоположна движению тела. Это обстоятельство и другие соображения позволяют предложить общую формулу работы постоянной силы при равномерном прямолинейном движении. Если сила и вектор смещения образуют между собой угол а, то работа этой силы равна произведению модуля силы на модуль смещения и косинуса угла между ними.
Это общее выражение для работы постоянной силы.
Из этой формулы видно, что в случае, когда угол между направлением вектора силы и вектором смещения острый, то косинус этого угла будет больше нуля и, следовательно, работа силы будет больше, чем нуль.
Если вектор силы и вектор смещения составляют тупой угол друг с другом, то значение косинуса этого угла меньше нуля. Это означает, что работа этой силы будет отрицательной.
И, наконец, если вектор силы перпендикулярен вектору перемещения, то работа не совершается (вернее, работа этой силы равна нулю).
Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работы отдельных сил.