Если вам известен коэффициент Pf (cos φ), вы можете рассчитать номинальную мощность потребителя электроэнергии по его номинальному напряжению, умноженному на величину потребляемого им тока.
Что такое реактивная мощность и как её рассчитать?
Давайте сначала рассмотрим понятие электричества. В самом широком смысле этот термин относится к работе, выполняемой в единицу времени. В контексте электроэнергии термин мощность несколько видоизменяется: Электрическая мощность — это физическая величина, которая описывает скорость выработки электроэнергии или количество переданной или потребленной электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, которая измеряется в ваттах. Мгновенная мощность на участке цепи задается формулой: P = U×I, где U и I — мгновенные значения параметров напряжения и тока на данном участке.
Строго говоря, приведенная выше формула применима только к постоянному току. Однако в синусоидальных цепях формула работает только в том случае, если нагрузка потребителей является чисто активной. При резистивной нагрузке весь ток используется для совершения полезной работы. Примерами активных нагрузок являются резистивные устройства, такие как кипящий водонагреватель или лампочка.
Когда в цепи присутствуют емкостные или индуктивные нагрузки, возникают паразитные токи, которые не способствуют полезной работе. Сила этих токов называется реактивным током.
При индуктивной и емкостной нагрузках часть электрической энергии теряется в виде тепла, а часть препятствует выполнению полезной работы.
Физика процесса
В цепях постоянного тока вопрос о реактивной мощности не возникает. В таких цепях значения мгновенной и кажущейся мощности идентичны. Исключением являются емкостные и индуктивные нагрузки, которые включаются и выключаются.
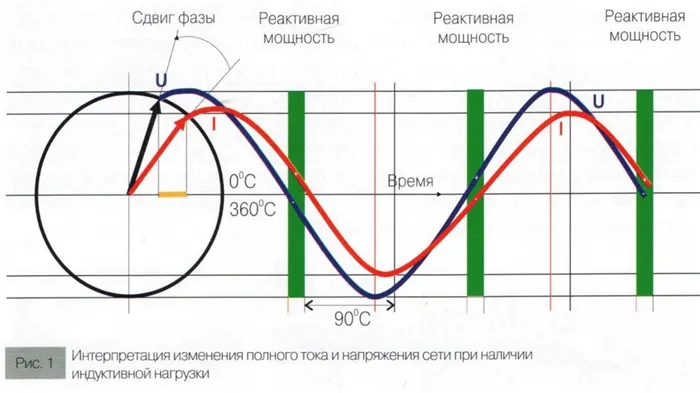
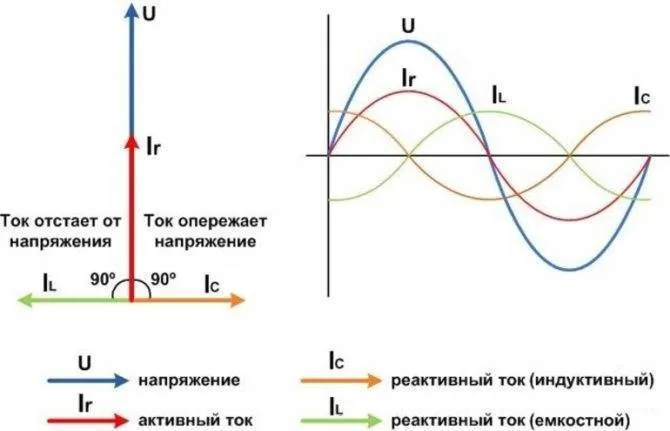
Аналогичная ситуация с чисто активными резисторами в синусоидальных цепях. Однако если такая цепь содержит устройства с индуктивными или емкостными сопротивлениями, происходит сдвиг фаз тока и напряжения (см. рис. 1).
У индукторов фаза тока запаздывает, тогда как у конденсаторов фаза тока сдвинута так, что ток опережает напряжение. Из-за помех, вызванных гармониками тока, полная мощность разделяется на две составляющие. Емкостные и индуктивные компоненты называются реактивными компонентами отходов. Второй компонент состоит из активной мощности.
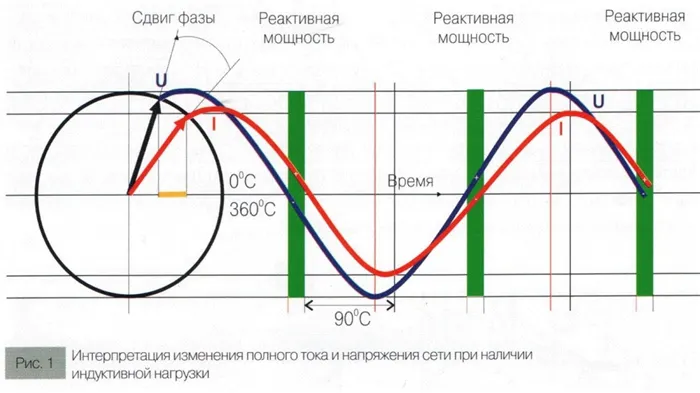
Рисунок 1: Сдвиг фазы при индуктивной нагрузке
Фазовый угол используется при расчете активных и реактивных емкостных или индуктивных сил. Если угол φ = 0, как в случае с резистивными нагрузками, то активная составляющая отсутствует.
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Источник реактивной энергии
Чтобы понять природу этой энергии и определить реактивную мощность, необходимо знать, что любая электромагнитная или индуктивная машина, работающая на переменном токе, преобразует электрическую энергию в тепловую. Для того чтобы это преобразование произошло, необходимо магнитное поле. Поэтому он образуется из энергии без воды. Причина этого заключается в том, что индукционная цепь поглощает и высвобождает энергию, когда магнитное поле уменьшается дважды за цикл сетевой частоты.

Природа явления
Понятие о реактивной мощности
Чтобы знать, что такое реактивная мощность, необходимо знать другие возможные формы мощности. Когда в цепи есть активная нагрузка (резистор), потребляется чистая активная мощность, которая полностью рассеивается. Таким образом, мы можем сформулировать, что такое активная мощность, т.е. мощность, при которой ток совершает эффективную работу.
При постоянном токе потребляется только активная мощность, которая рассчитывается по формуле:
Он измеряется в ваттах (Вт).
В цепях переменного тока с активной и реактивной нагрузками выходная мощность является суммой этих двух составляющих: Активная и реактивная мощность.
Существует два типа реактивных нагрузок:
- Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
- Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.
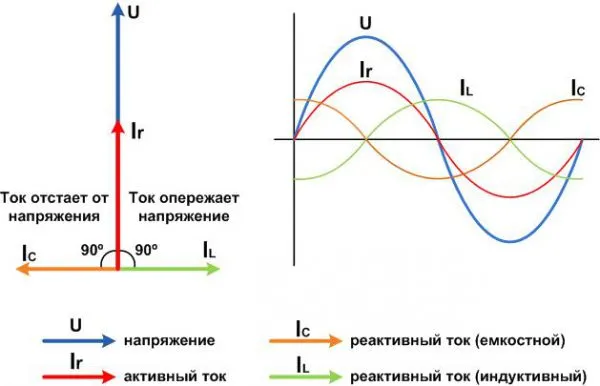
Емкостные и индуктивные нагрузки.
Если рассматривать цепь с переменным током и подключенной активной нагрузкой (нагреватели, чайники, свечи накаливания), то ток и напряжение находятся в фазе, а полная мощность, полученная при данном временном перерыве, рассчитывается путем перемножения составляющих напряжения и тока.
Однако если цепь содержит реактивные элементы, то значения напряжения и тока не синфазны, а отличаются на величину, определяемую углом смещения «φ». Проще говоря, это означает, что реактивная нагрузка возвращает в цепь столько энергии, сколько потребляет. В результате показатель активного энергопотребления будет равен нулю. В то же время в цепи протекает реактивный ток, который не совершает никакой эффективной работы. Следовательно, потребляется реактивная мощность.
Реактивная мощность — это часть энергии, которая позволяет регулировать электромагнитные поля, необходимые устройствам переменного тока.
Реактивная мощность рассчитывается по следующей формуле:
Q = U x I x sin φ.
Единицей измерения реактивной мощности является VAR (реактивный вольт-ампер).
Выражение для активной мощности:
P = U x I x cos φ.
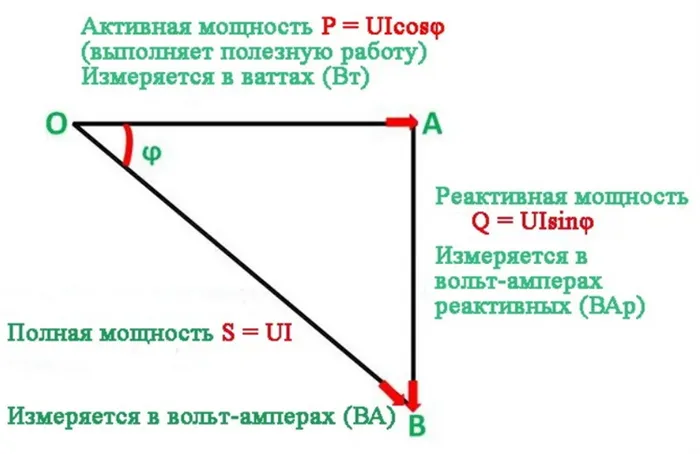
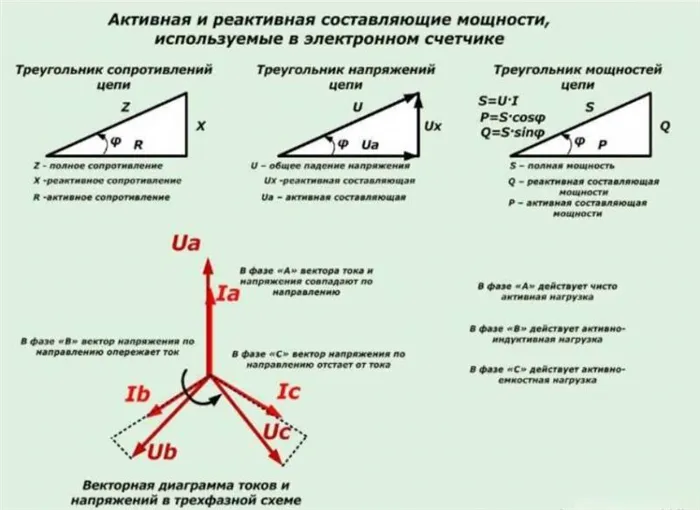
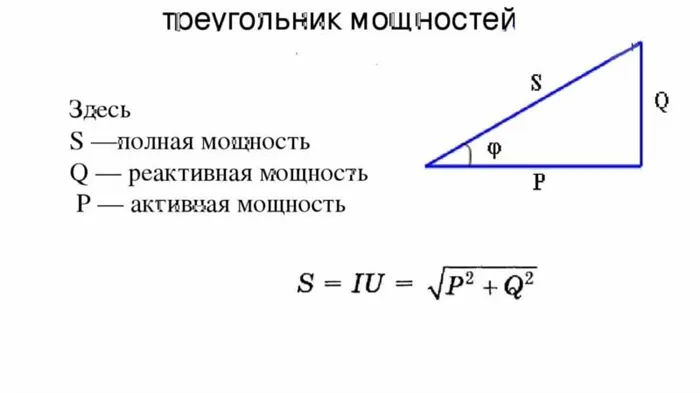
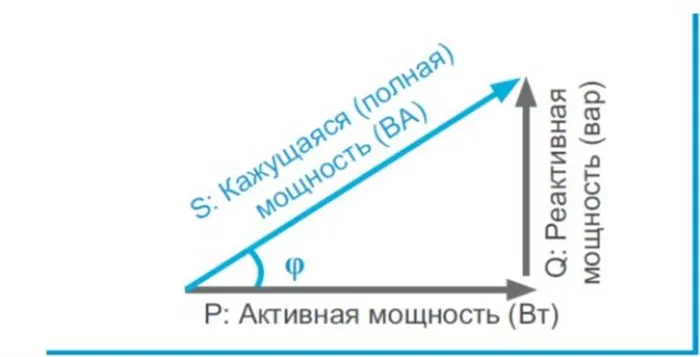
Треугольник мощностей
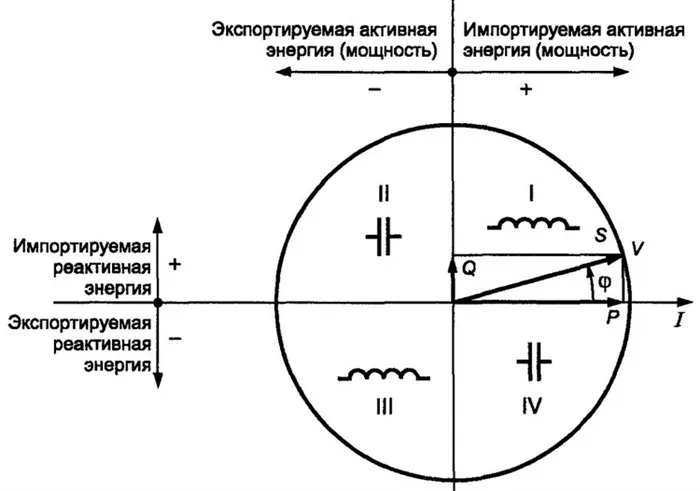
Взаимосвязь между активной, реактивной и кажущейся мощностью в синусоидальном переменном токе геометрически представлена тремя сторонами прямоугольного треугольника, так называемого треугольника мощности. Цепи переменного тока потребляют два вида энергии: активную мощность и реактивную мощность. Кроме того, значение активной мощности никогда не бывает отрицательным, в то время как для реактивной мощности возможно как положительное значение (для индуктивных нагрузок), так и отрицательное (для емкостных нагрузок).
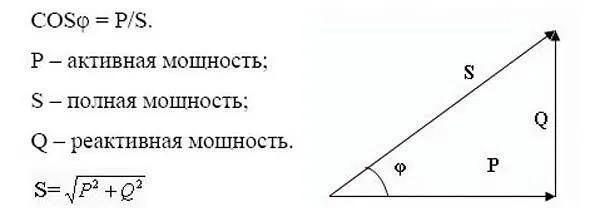
Это важно: из треугольника мощности следует, что всегда имеет смысл уменьшать реактивную составляющую, чтобы повысить эффективность системы.
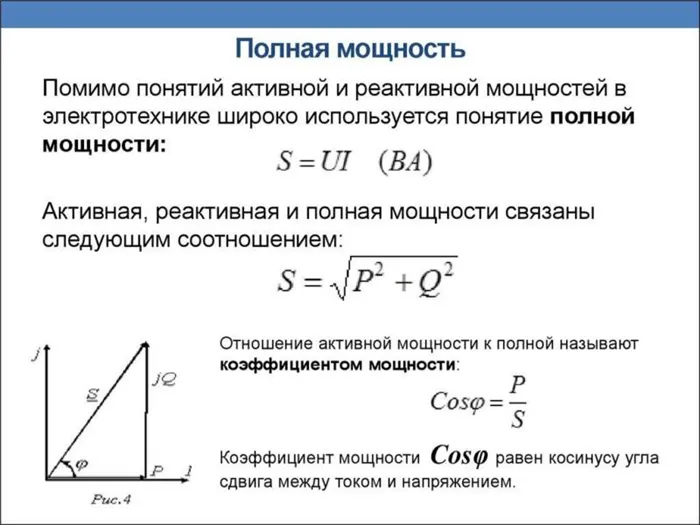
Полная мощность определяется не как алгебраическая сумма значений активной и реактивной мощности, а как векторная сумма P и Q. Она рассчитывается путем взятия квадратного корня из значений активной и реактивной мощности. Она определяется квадратным корнем из суммы квадратов значений активной и реактивной мощности. Полная мощность может быть измерена в ВА (вольт-амперах) или их производных: кВА, мВА.
Для расчета кажущейся мощности необходимо знать разность фаз между синусоидальными значениями U и I.
Коэффициент мощности
Геометрическая векторная диаграмма может быть использована для определения отношения сторон треугольника, соответствующих активной и кажущейся мощности, что соответствует косинусу phi или коэффициенту мощности:
Этот коэффициент определяет эффективность сети.
Количество потребляемых ватт равно количеству потребляемых вольт при коэффициенте мощности 1 или 100 %.
Чем больше cos φ или чем меньше угол изменения синусоидальных значений тока и напряжения, тем ближе полная мощность к активной мощности.
Например, если есть катушка, для которой:
- Р = 80 Вт;
- Q = 130 ВАр;
- тогда S = 152,6 BA как среднеквадратичный показатель;
- cos φ = P/S = 0,52 или 52%
Мы можем предположить, что для выполнения 80 Вт полезной работы катушке требуется 130 ВАр полной мощности.
Треугольник мощностей
Чтобы понять, что такое реактивная нагрузка, рассмотрим треугольник мощности.
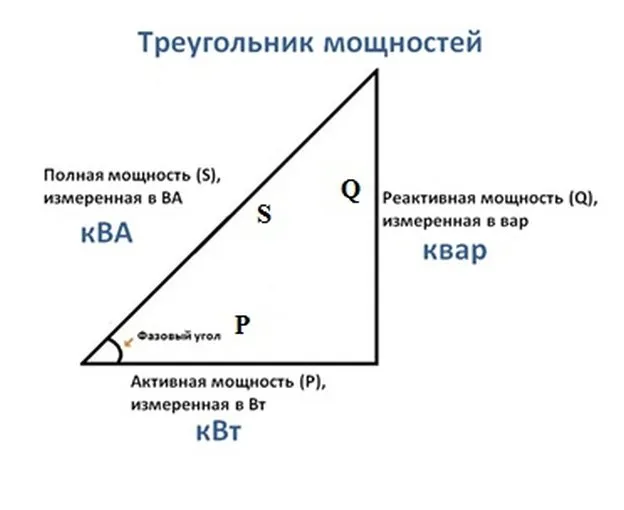
Здесь P — активная мощность, измеряемая в ваттах, используемая для выполнения полезной работы,
Q — реактивная мощность, которая измеряется в ваттах и используется для генерации электромагнитного поля,
S — полная мощность, которая используется для расчета электрических цепей.
Чтобы рассчитать полную мощность, примените теорему Пифагора: S 2 =P 2 +Q 2. Или можно использовать формулу: S=U*I, где U — напряжение, считанное на нагрузке, а I — показания амперметра, подключенного последовательно с нагрузкой. Коэффициент мощности — cosφ — также включается в расчеты. Приборы, обозначающие реактивные нагрузки, обычно указывают активную мощность и cosφ. С помощью этих параметров можно также определить кажущуюся мощность.
Иногда на измерительном приборе отображается полная мощность, но не cosφ. В этом случае применяется коэффициент 0,7.
Нелинейная нагрузка
Его особенность в том, что напряжение и ток не пропорциональны. К нелинейным нагрузкам относятся телевизоры, музыкальное оборудование, электронные настольные часы, компьютеры и их компоненты. Сама нелинейность обусловлена тем, что в этом электронном устройстве используются импульсные источники питания. Пик синусоидальной волны достаточен для зарядки конденсатора в импульсном источнике питания.
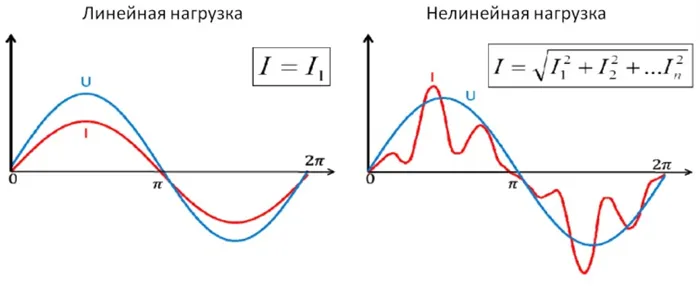
В остальное время конденсатор не потребляет ток из сети. В этом случае ток имеет импульсное качество. К чему все это приведет? Это приводит к искажению синусоидальной волны. Но не все электронные устройства работают с искаженной синусоидой. Проблема решается с помощью регуляторов двойного преобразования, в которых питание от сети преобразуется в постоянный ток. Затем он преобразуется из постоянного тока в переменный ток нужной формы и амплитуды.
Пусковой ток
При расчете необходимо также учитывать входные токи устройства. Например, сопротивление нити накала лампы при включении в 10 раз меньше, чем во время работы. Следовательно, пусковой ток этой лампы в 10 раз выше. Через определенное время она начинает поглощать энергию, накопленную в данных этой лампы. Поэтому он перегорит из-за высоких пусковых токов при включении.
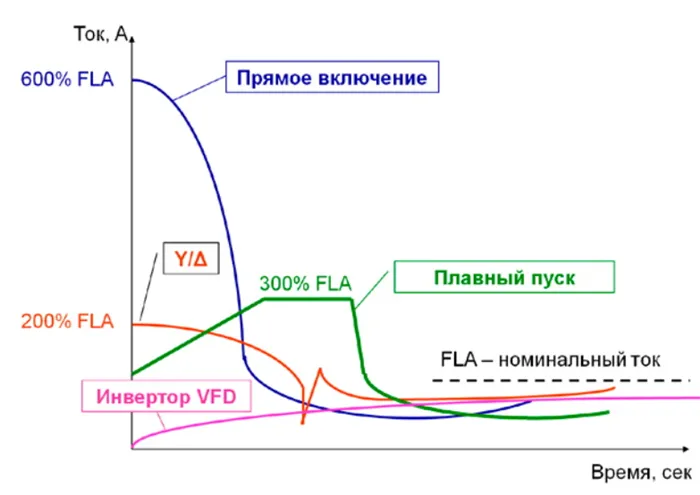
В электронных устройствах также возникает пусковой ток, пока не зарядится конденсатор в источнике питания.
Аналогично, входной ток двигателя генерируется до тех пор, пока двигатель не достигнет номинальной скорости.
В нагревателях пусковой ток генерируется до тех пор, пока катушка не достигнет температуры ожидания.
Треугольник мощностей
Формула для расчета кажущейся мощности, активной мощности и реактивной мощности может четко описать взаимосвязь между этими тремя аспектами. Но еще более наглядно их отношения можно представить на плоскости в виде силового треугольника. Поскольку все связано тригонометрически. Угол, образующийся между полной мощностью и активной мощностью, называется фазовым углом и хорошо виден на рисунке.
См. также: флуоресцентные трубки ручной работы: Построение и подключение 12-вольтовой светодиодной цепи.
Формулы и единицы измерения
Единица измерения реактивной мощности такая же, как и для полной мощности — вольт-ампер, VAR, в то время как единица, используемая для расчета активной мощности, выражается в ваттах.

Комбинация активной и реактивной мощности называется кажущейся мощностью. Он рассчитывается по следующей простой формуле:
√ (активная мощность2 + реактивная мощность2).
То есть, необходимо найти квадратный корень из суммы квадрата активной мощности и квадрата реактивной мощности.
Как найти реактивную мощность:
√ (полная мощность2 — активная мощность2).
То есть, квадратный корень из квадрата активной мощности, деленный на квадрат кажущейся мощности. Для расчета активной мощности применяется соответствующая формула:
√ (валовая мощность2 — активная мощность2)
Квадрат квадрата реактивной мощности, вычтенный из квадрата кажущейся мощности.

Для точных расчетов в некоторых случаях могут потребоваться другие формулы. Для однофазных цепей можно использовать отдельную формулу:
Однако в трехфазных цепях уже действует следующее:
P = √3 VL IL cos θ
Это важно: в любом случае обращайте внимание на единицы измерения. Перед расчетом по формулам необходимо перевести киловатты в ватты. Киловольт-амперы преобразуются в вольт-амперы соответствующим образом.
Как найти активную, реактивную и полную мощность
Коэффициент реактивной мощности позволяет оптимизировать работу и предотвратить нагрев устройства. Эксперты обычно используют больше параметров в своих расчетах, чтобы компенсировать негативные аспекты реактивной мощности. Но для обычных физических задач приведенная выше формула вполне применима.
Полная мощность, реальная мощность и реактивная мощность для чайников могут быть представлены различными формулами. Важно только запомнить законные единицы измерения, текущие обозначения и треугольник мощности, чтобы справиться с расчетами.

Определения
Каждый электроприбор, подключенный к электросети, работает на переменном токе. Это утверждение важно, потому что именно в этих условиях мы в следующий раз будем иметь дело с «властью».

Мощность — это физическая величина, указывающая на скорость передачи или преобразования электроэнергии. В качестве альтернативы этот термин объясняется как отношение работы к определенному времени, за которое эта работа была выполнена.
Термин «мощность» можно объяснить более подробно на примере обычной лампочки. Лампочка потребляет электричество, а скорость, с которой оно преобразуется в свет или тепло, является мощностью лампочки.

Отсюда также можно сделать вывод, что чем больше выходная мощность устройства (в данном случае лампы), тем больше электроэнергии оно потребляет и тем больше света излучает.

Активная мощность
Активная мощность — это мощность, которая конкретно описывает процесс преобразования электрической энергии во что-то другое. Он измеряется в ваттах (Вт) и обозначается буквой P.

Активная энергия используется на термоэлектростанциях и атомных электростанциях, поскольку именно там вырабатывается напряжение, которое затем подается в наши дома для потребления, позволяя всем электроприборам работать на электричестве.
Реактивная мощность
Реактивная мощность — это физическая величина, которая является свойством нагрузки, возникающей в устройствах цепи из-за изменения энергии электромагнитного поля.

Это явление возникает в цепи с переменным током. Из этого также вытекает зависимость: мощность равна произведению среднеквадратичных значений тока и напряжения. Более подробно эта формула будет описана в следующей главе.

Наиболее важным различием между реактивными нагрузками является индуктивность и емкость. Другими словами, это способность накапливать энергию, чтобы позже вернуть ее в сеть.

Энергия электрического тока сначала преобразуется индуктивной нагрузкой в магнитное поле, а затем в электрический ток. Пример: электромагниты, трансформаторы, асинхронные двигатели.

Как и индуктивная нагрузка, емкостная нагрузка также преобразует энергию тока в электрическое поле, но не в магнитное поле. Затем он снова преобразуется в электрический ток. Оба процесса воспроизводятся в течение одной секунды в полукруге. Примерами являются современные двигатели, батареи и конденсаторы.
Физическое объединение реактивной и активной мощности
Существует такая вещь, как «полная власть». Этот показатель можно рассчитать геометрически, так как он равен квадратному корню из суммы квадратов реактивной и активной мощности. Он обозначается S и выражается в вольт-амперах (ВА).

В физике существует «силовой треугольник», иллюстрирующий взаимосвязь между всеми силами — соотношение активных, реактивных и кажущихся сил.
Первое, что нужно сделать, это представить себе прямоугольный треугольник, где щупы представляют активную и реактивную мощность, а гипотенуза — полную мощность. Согласно законам геометрии, косинус угла phi равен отношению реактивной и активной мощности, т.е. коэффициенту мощности.
Этот коэффициент рассчитывается в диапазоне от нуля до единицы, или, выраженный в процентах, от нуля процентов до ста. Чем выше активная мощность, тем выше коэффициент и тем лучше производительность устройства.
Формулы для нахождения мощностей
В большинстве случаев активная мощность и числовое значение коэффициента косинус-фи указываются на электрооборудовании. Если такие данные имеются, легко рассчитать необходимые значения.

Формула кажущейся мощности основана на умножении тока и напряжения:
- S = UxI, где
- S – полная мощность,
- U – электрическое напряжение,
- I – сила тока.
Реактивная мощность обозначается буквой P и рассчитывается в вольтах (Вт), а вместе с активной мощностью она дает полную мощность:
На практике, однако, эта формула будет найдена другим способом:

Иногда для поиска мощности могут потребоваться емкостные и индуктивные нагрузки. Следует отметить, что для индуктивной нагрузки точка на кривой всегда находится на полсекунды дальше от кривой напряжения. В то же время, для емкостной нагрузки точка на кривой опережает кривую напряжения на полпериода.

На практике коэффициент фи-косинуса обычно указывается в описании устройства, но если вам нужно измерить его самостоятельно, можно воспользоваться спектрометром или цифровым вольтметром. Оба способа значительно упрощают различные расчеты, хотя для более точного теоретического расчета рекомендуется использовать формулы.
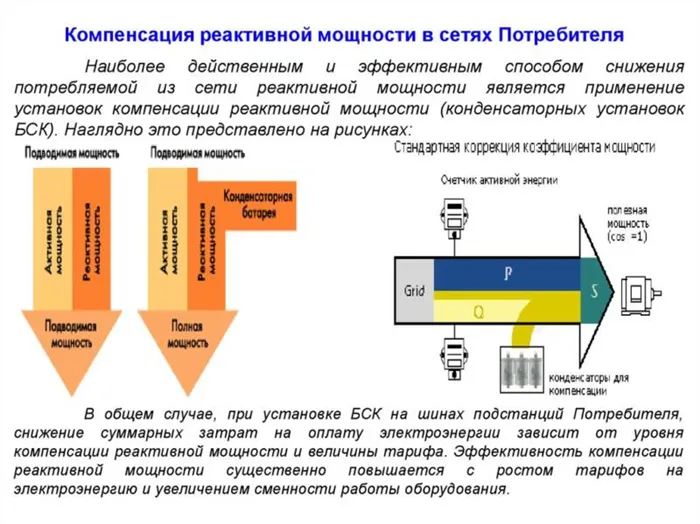
Расчет коэффициента мощности необходим для компенсации недостатка коэффициента мощности путем добавления в цепь дополнительных элементов.

Иногда может потребоваться компенсация реактивной мощности. Это делается путем добавления в цепь реактивного устройства, выполняющего функцию, противоположную функции уже работающей электрической системы. Например, для компенсации работы асинхронного двигателя параллельно подключается конденсатор. Работа синхронного двигателя компенсируется электромагнитом.
Из того, что мы узнали, можно сделать вывод, что активная и реактивная мощность неразделимы, но не противоположны друг другу. Вместе они образуют другой термин «полная мощность», а также позволяют вычислить косинус коэффициента phi.

Мощность (активная, реактивная или кажущаяся) является наиболее важным понятием в физике, как в теории, так и на практике. Знать, что означают эти величины и как их рассчитать (с помощью формул или специальных приборов), интересно и важно не только для студентов или инженеров, но и для обычных людей, которые развиваются целостно