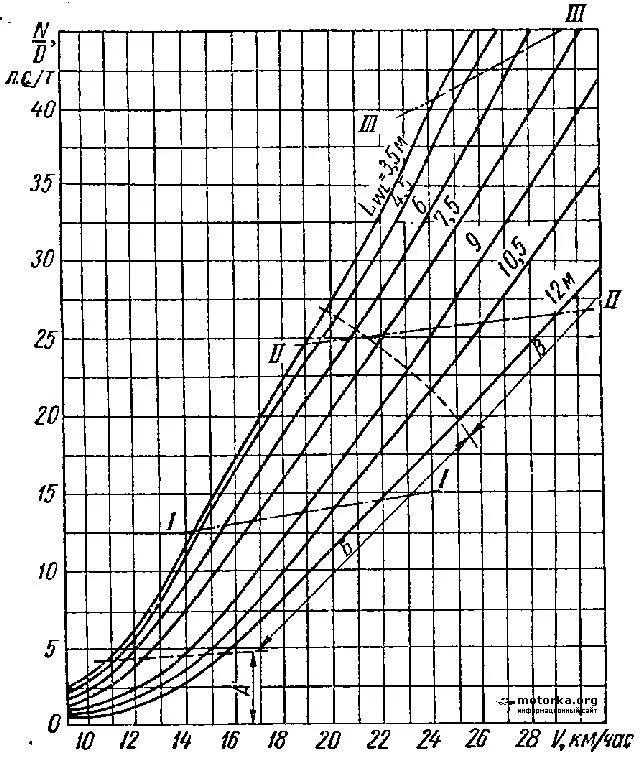
Это показывает, что катер с длиной ватерлинии 15 м и водоизмещением 10 тонн должен двигаться со скоростью 20 км/ч с двигателем мощностью 50 л.с. и 16 км/ч с двигателем мощностью 25 л.с. Как правило, двигатель может плавать при 0 л.с., что означает, что что-то не так.
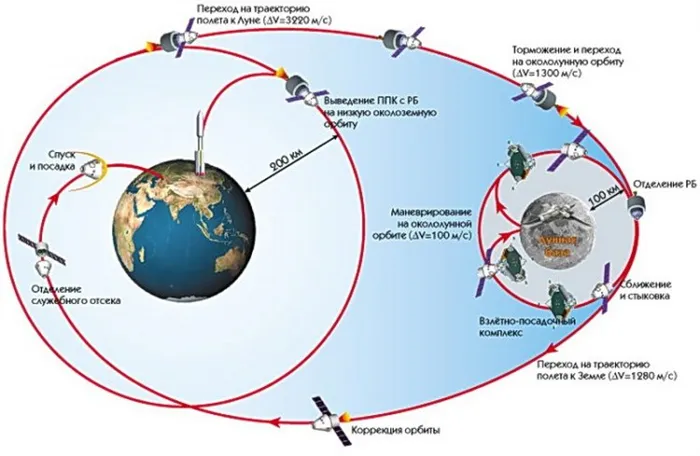
Зависимость скорости судна от его формы и мощности мотора в водоизмеща
Сразу прошу прощения за вопрос нубский — может для профессионалов он звучит глупо и именно такими вещами измеряется голова, но прошу помочь мне с решением или кинуть мне ссылку на него.
Вопрос к строителям лодок и катеров.
Меня интересует простая формула для нахождения мощности, необходимой на гребном валу для лодки определенной формы в водоизмещающем режиме на определенной скорости. Или наоборот — если известна определенная мощность винта, то известно, какой скорости может достичь лодка определенной формы.
Меня интересует теоретическое решение этой проблемы. Я понимаю, что существует простая формула, в которую нужно только вставить правильные коэффициенты.
Предположим, что условия следующие:
— Режим вытеснения
— Суда с длиной ватерлинии от 10 до 15 метров (30-50 футов).
— Оптимальный гребной винт для заданной скорости и оборотов двигателя. (например, эффективность 50-60%;)
— Водоизмещение 4-15 тонн.
Что касается сопротивления и формы корпуса, вас интересуют стандартные данные или коэффициенты для:
— Скользящее судно в водоизмещающем режиме
— Судно с оптимальной формой для водоизмещающего режима
— Плавание на круизном катамаране
— Типичное круизное судно
Все они имеют длину 30-50 футов.
То есть, при определенных условиях мы хотели бы иметь формулу, по которой, подставив некоторые цифры, мы можем сказать, что лодка с длиной ватерлинии A и водоизмещением B будет плыть со скоростью X узлов при мощности двигателя 20 л.с. И наоборот, если вы поставите двигатель мощностью 15 л.с., он сможет делать Y узлов. Конечно, погрешность +-20% вполне допустима.
Существует ли такая формула и коэффициенты?
#4 Ильяф Иллер
Наглая рыжая морда. +79116333662
Наберите в Google «число Фруда».
Рулевой 1 класса.
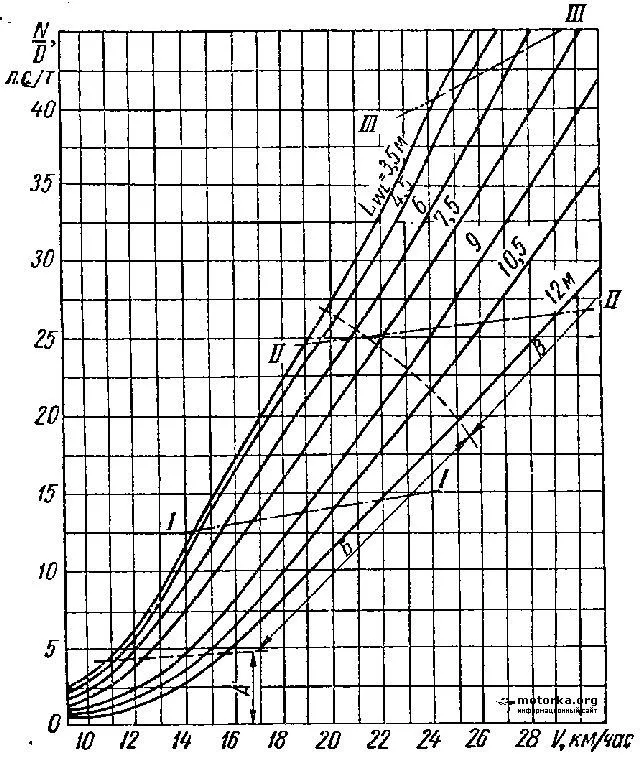
Просто проблема всех этих графиков в том, что меня интересует нижняя левая часть графика — когда мощность мотора составляет менее 5 л/с на тонну. Получается, что можно уменьшать мощность дальше, а скорость все равно будет более 10км/ч для длин ватерлинии > 10м.
Например, если взять кривую для длины 10,5 м, то мощность двигателя при скорости 10 км/ч может быть следующей.
Сообщение отредактировал syoma: 30 Октябрь 2020 — 15:36.
#6 Albert Nazarov
Просто проблема всех этих графиков в том, что меня интересует нижняя левая часть графика — когда мощность мотора составляет менее 5 л/с на тонну. Получается, что можно уменьшать мощность дальше, а скорость все равно будет более 10км/ч для длин ватерлинии > 10м.
Например, если взять кривую для длины 10,5 м, то мощность двигателя при скорости 10 км/ч может быть следующей.
При очень низкой мощности скорость сильно зависит от внешних факторов. Например, состояние ветра и моря. Сопротивление воздуха (и, следовательно, мощность) может измениться в 2 и более раз.
Сила, под действием которой тело притягивается к земле, называется гравитацией. Падение тела в воздушном пространстве под действием силы тяжести (при нахождении тела в воздухе коэффициент 0 = 0) называется свободным падением.
Чем быстрее мы идем, тем больше нужно колоссальной энергии …
Поэтому самые живые умы уже предполагают, что я упомяну знаменитую формулу: кинетическая энергия = 1/2 X масса X скорость² (или, выражаясь более синтетически, E = 1 / 2.M.V²). Это уравнение заставляет нас выяснить, как кинетическая энергия изменяется со скоростью, и таким образом мы можем наблюдать, является ли она линейной, убывающей или прогрессирующей. Поэтому мы немного поиграем с ним, чтобы лучше понять его.
Однако позвольте мне коротко напомнить вам, что это уравнение Ньютона, которое не работает, когда мы приближаемся к крайним значениям (слишком большая масса или скорость), поэтому мы должны обратиться к Эйнштейну, который улучшил это уравнение, чтобы сделать его еще более точным (опасно говорить о точности, потому что мы все еще далеки от полного раскрытия природы, и уравнения Эйнштейна тоже когда-нибудь отойдут на второй план).
Вот он.
С Y, который является не неизвестным, а небольшой частью другого уравнения без неизвестного.
Детали условий
- Кинетическая энергия: в джоулях (также используется для измерения тепла и в более общем смысле для измерения различных сил, которые мы наблюдаем и испытываем в природе). Кинетическая энергия — это запасенная энергия, связанная со скоростью движения массы. Инерция показывает, насколько трудно сдвинуть массу: чем она больше (точнее, чем больше масса), тем труднее ее сдвинуть. И природа создала очень странную взаимосвязь, гравитация и инерционная масса идеально синхронизированы (результат: все падает с одинаковой скоростью)… То, что Луна и Солнце одинакового размера на небе, очень тревожит. Совпадение, как и переменные вселенной, которые идеально выверены (масса и заряд элементарных частиц, для небольшого примера), поэтому мы можем наблюдать появление вещей, которые имеют смысл (что некоторые приписывают существованию Творца…). Малейшее изменение любой из этих переменных приводит к тому, что Вселенная не производит ничего, кроме огромного «супа» частиц, из которого не может возникнуть ничего связного (например, атома).
- Масса: вес в килограммах (варьируется от планеты к планете, в отличие от инерционной массы. Эти веса меняются, например, на Луне).
- Vitesse : в метрах в секунду (пересчитывается, когда мы начинаем с км/ч).
В чем проблема?
Прежде чем разобраться, о чем идет речь, давайте проясним суть проблемы: Почему для разгона с 200 до 220 км/ч требуется больше энергии, чем для разгона со 180 до 200 км/ч? В обоих случаях я хочу на 20 км/ч больше, это должно быть одинаковое требование (представьте себе прогулку по Луне без атмосферы, замутняющей воду).

Мы не имеем здесь дело с зубчатыми колесами, что очень затруднило бы измерения и выводы, но мы предполагаем, что существует только одна постоянная взаимосвязь. То же самое относится и к аэродинамике, которую мы оставили без внимания. Итак, мы собираемся исследовать, что даст эволюция кинетической энергии без каких-либо других аэродинамических ограничений или передач, т.е. это все равно, что управлять автомобилем на Луне без передач.
Конкретные примеры
Автомобиль 1000 кг
Давайте посмотрим, с чего начинает автомобиль весом 1000 кг. 70 км/ч (= 19,4 м/с):
Ec = 1/2 X 1000 X 19,4²
Ec = 188 180 джоулей
Посмотрим, это дает 140 км/ч, вдвое большую скорость:
Ec = 1/2 X 1000 X 38,8²
Ec = 752 720 джоулей
Таким образом, мы видим, что для 4-кратного увеличения скорости нам нужно в 2 раза больше энергии / рабочей силы …
Эта рабочая сила может модулироваться переменными времени и силы: Чем больше времени я дам себе на достижение этой скорости, тем меньше энергии мне понадобится. Но если вы жертвуете одним, вы отказываетесь от другого: Слишком сильное снижение мощности делает практически невозможным достижение желаемой скорости (период времени, который может занять почти вечность).
Одним словом, объем работы, необходимый для достижения скорости, изменяется экспоненциально. И мощность двигателя достигнет этого более или менее быстро, если вообще достигнет, если приложенная сила (количество работы) очень мала по отношению к массе объекта.
Автомобиль 2500 кг
Давайте возьмем большой внедорожник класса люкс весом 2 500 кг и немного сравним результаты с маленьким автомобилем весом 1 000 кг, который мы видели ранее (снова на скорости 70 км/ч):
Ec = 1/2 X 2500 X 19,4²
Ec = 470 450 Дж
Как и следовало ожидать, она пропорциональна топовому Twingo: джоули пропорциональны массе (188 180 джоулей x 2,5 = 470 450 джоулей). Необходимая энергия изменяется экспоненциально со скоростью (которая в уравнении возводится в квадрат), но линейно и пропорционально массе (которая, следовательно, в уравнении не возводится в квадрат).
A 140 км/ч :
Ec = 1/2 X 2500 X 38,8²
Ec = 1 джоуль
F = ma = ( mυ 2 — мЮ 1) / ( t 2 — t 1) = ( ∆ ( m u ) ) / ∆ t
Что такое силовая тренировка?
Целью силовых тренировок является улучшение способности преодолевать сопротивление, перемещая как можно больший вес за заданное количество повторений. Акцент делается на перемещении веса из одной точки пространства в другую. Если взять в качестве примера оборудование для силовых тренировок, то такими точками будут верхнее и нижнее положение противовеса или край растягиваемой и сжимаемой пружины.
Этот вид тренировок подходит не только для тех, кто хочет нарастить мышечную массу и увеличить свои объемы. Сила необходима для выполнения многих повседневных задач в жизни человека. Любое действие дается легче, когда у вас есть сила в мышцах. То же самое верно и для освоения любого вида спорта.
Тренировка мощности
Силовые тренировки — это не только преодоление сопротивления, но и способность преодолеть это сопротивление в кратчайшие сроки.
Поскольку мощность — это сила, умноженная на скорость (см. формулу выше), мощность можно увеличить двумя способами:
- путем увеличения силы
- путем увеличения скорости.
Чтобы максимально развить силу и разнообразить тренировки, можно использовать комбинацию упражнений в диапазоне от нуля до 90% от максимального количества повторений (1ПМ) и таким образом задействовать почти весь потенциал производительности.
Силовые тренировки развивают скоростные и силовые навыки, требующие высокой скорости движений при сохранении силы. Примеры скоростно-силовых видов спорта: легкая атлетика (спринт, прыжки и метания), боевые искусства (бокс, кикбоксинг, тхэквондо), тяжелая атлетика (пауэрлифтинг). Некоторые из этих проявлений скоростной силы называются взрывной силой.