Треугольник в звезду. Преобразование из треугольника в звезду.

Поскольку это значение находится между минимальным и максимальным пределами, мы абсолютно уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ достаточно близок к правильному. Таким образом, полный ток равен

Преобразование треугольник/звезда: что за сценой?

Преобразования дельта/звезда позволяют заменить часть схемы другой схемой с эквивалентным поведением, но могут значительно упростить анализ всей схемы. Здесь мы узнаем, откуда берутся эти преобразования.

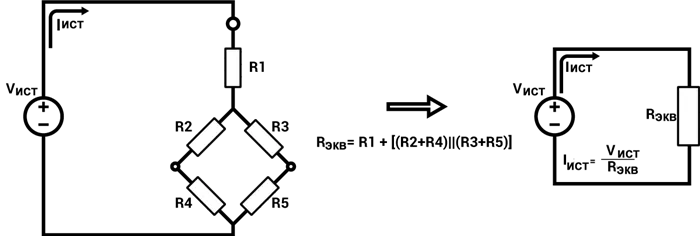
Когда мы начинали изучать электронику, резисторы соединялись либо последовательно, либо параллельно, и мы учились заменять такие комбинации их эквивалентными резисторами, часто с целью свести всю сеть резисторов к одному эквивалентному резистору, видимому из источника питания. Впоследствии появились схемы (рис. 1), содержащие резисторы, которые не были ни последовательными, ни параллельными, но их можно было удалить путем тщательной идентификации и приведения частей схемы к правильной последовательности. Обратите внимание, что R₁ни параллельно, ни последовательно с R₂ни с R₃но, объединив R₂последовательно с R₄и комбинация R₃последовательно с R₅затем мы можем соединить два эквивалентных резистора параллельно и, наконец, результат последовательно с R₁мы получим общее сопротивление источника питания, которое с помощью закона Ома поможет нам найти общий ток источника питания.

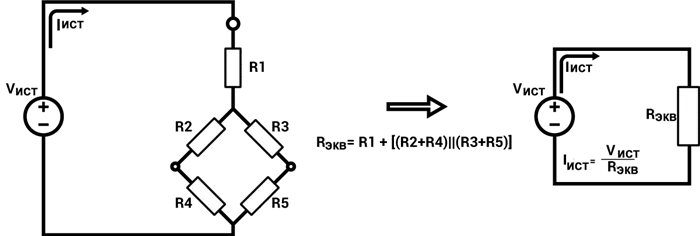
Но теперь мы приходим к схемам (рис. 2), где нет пар резисторов последовательно или параллельно — кажется, мы зашли в тупик. Одним из способов анализа этой цепи является использование закона Кирхгофа для напряжений (второй закон) и закона Кирхгофа для токов (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход всегда работает (для этих и большинства других типов схем), он может быть довольно громоздким. Мы можем принять это как издержки анализа более сложных схем, но иногда мы можем избежать этих вычислений, изменив или «преобразовав» части схемы так, чтобы превратить ее в нечто, что мы можем уменьшить только с помощью правил последовательного/параллельного соотношения.

Для простоты мы рассматриваем только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Чтобы сосредоточить обсуждение на преобразованиях, определяется только общий ток, подаваемый источником напряжения, что означает, что вся сеть резисторов должна быть сведена к одному эквивалентному резистору.

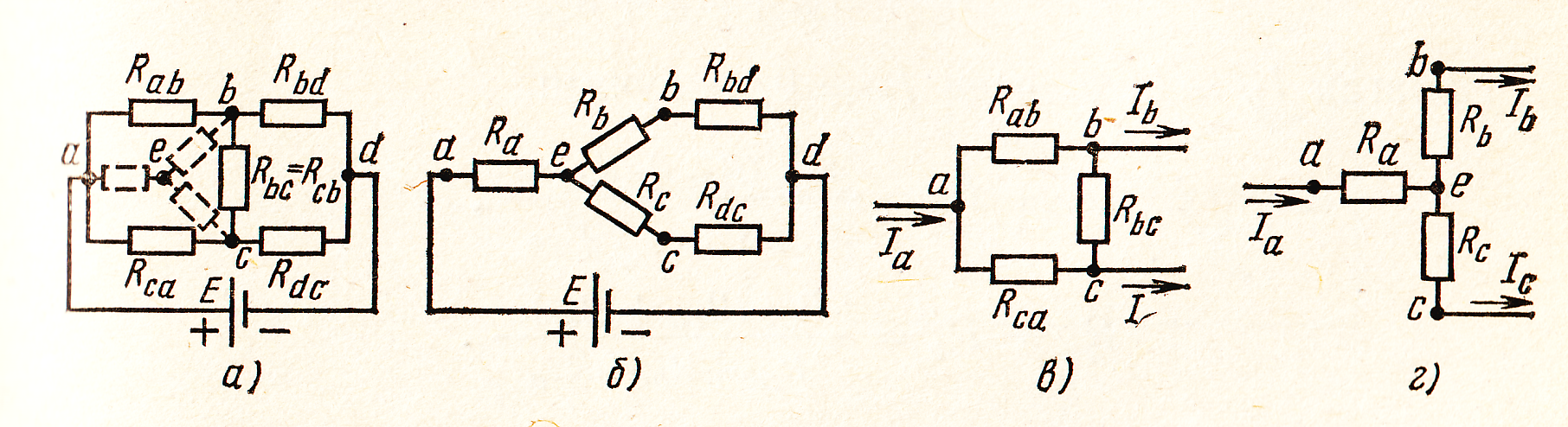
Если мы рассмотрим эти две схемы немного ближе (рис. 3), то увидим, что единственное различие между ними заключается в том, что находится в пунктирных кружках. В каждом случае цепь в круге имеет три контакта, которые пересекают круг и взаимодействуют с остальной частью цепи. В схеме слева (рис. 3(a)) резисторы подключены к контактам по схеме «треугольник» (в англоязычной литературе «треугольник», названной в честь греческой заглавной буквы D), а в схеме справа — по схеме «звезда» (в англоязычной литературе «звезда», названной в честь английской заглавной буквы Y, но перевернутой на схеме).

Основные соотношения

Чтобы определить уравнения, соединяющие резисторы в схеме «треугольник» с резисторами в схеме «звезда», нам понадобятся только проверенные формулы для последовательных/параллельных схем (и немного алгебры). Идея заключается в том, чтобы сбалансировать эквивалентные сопротивления между каждой парой контактов, при этом оставшийся контакт должен быть неподключенным (рис. 4).

Применив это к эквивалентному сопротивлению между контактами B-C, получим:

\R_B + R_C = \frac \left( R_ + R_ \right)>\

Если мы повторим эту процедуру для каждой другой пары контактов, то получим еще два подобных уравнения, каждое из которых дает необходимую нам информацию (при условии, что мы признаем симметрию).

Частный случай: симметричные схемы

Если сопротивления на каждом плече цепи, соединенной в треугольник или звезду, равны, такая цепь называется «симметричной». Это означает, что

\R_Y = R_A = R_B = R_C\.

Если мы объединим это условие с соотношением из предыдущего раздела, то сразу же получим уравнение преобразования для случая симметрии.

Причина этого довольно проста: когда инженеры разрабатывают схемы с треугольными или звездообразными соединениями, они часто пытаются сделать их симметричными. Поскольку это, конечно, не всегда возможно, мы должны быть в состоянии справиться с частым случаем, когда цепь не симметрична.

Треугольник в звезду

Расчет и исследование сложных электрических цепей во многих случаях может быть значительно облегчено и прояснено путем преобразования цепей одного типа в цепи другого типа. Одним из методов является преобразование в треугольно-звездном эквиваленте, при котором преобразуется пассивная часть цепи, т.е. приемники электрической энергии.

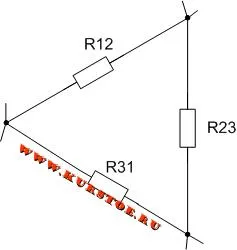
Если три резистора соединены так, что они образуют стороны треугольника, то такая цепь резисторов называется дельта-резистором.

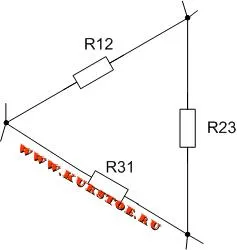
Соединение, в котором три резистора в пассивных ветвях соединены попарно, образуя замкнутую цепь, называется треугольником.

На занятиях по электротехнике принято рисовать элементы только горизонтально и вертикально. На следующей схеме также показана схема треугольника.

Причина преобразования треугольника в звезду

При расчете электрической цепи бывают случаи, когда нет последовательного или параллельного соединения резисторов. В этом случае можно попытаться найти соединение резистора треугольником и выполнить эквивалентное преобразование треугольник-звезда.

Если в схеме имеется соединение резисторов в форме треугольника, вставьте концы шин соединения резисторов в узлы соединения резисторов в форме звезды.

Затем удалите (удалите исходное дельта-соединение). В результате получается эквивалентное звездное соединение.

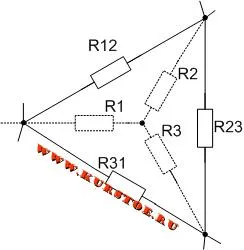
Формулы для расчета преобразования треугольника в звезду

Для схемы нам нужно преобразовать соединение треугольником R12 — R23 — R31 в соединение звездой.

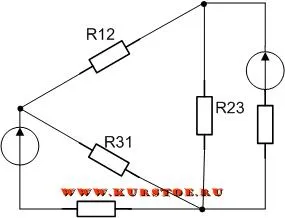
Подключите концы соединения «звезда» к резисторам «треугольник».

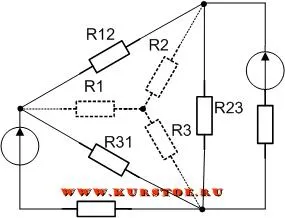
Удалите соединение треугольного резистора. Остается соединение резисторов звездой. Рассчитайте значения резисторов R1, R2, R3, используя формулы.

Лекции по ТОЭ

• История электротехники
• ТОЭ и электроника
• Основные сведения
  • Основные определения
  • Топология цепи
  • Преобразование цепей
  • Элементы электрической цепи
  • Режимы работы
  • Постояный ток
  • Переменный ток
  • Постоянный ток
  • Переменный ток
  • Мощность
  • Магнитное поле
  • Постоянная МДС
  • Переменная МДС
  • Ферромагнитные материалы
  • Однофазный трансформатор
  • Трехфазный трансформатор
  • Постоянный ток
  • Переменный ток
  • Электропривод
  • Параметры
  • Уравнения
  • Схемы замещения
  • Фильтры
  • Холостой ход
  • Короткое замыкание
  • Характеристическое сопротивление
  • Коэффициент распространения
  • Передаточная функция
  • Обратные связи
  • Общие сведения
  • Классический метод
  • Операторный метод
  • Интеграл Дюамеля
  • Основная литература
  • Дополнительная литература
  • Сборники задач

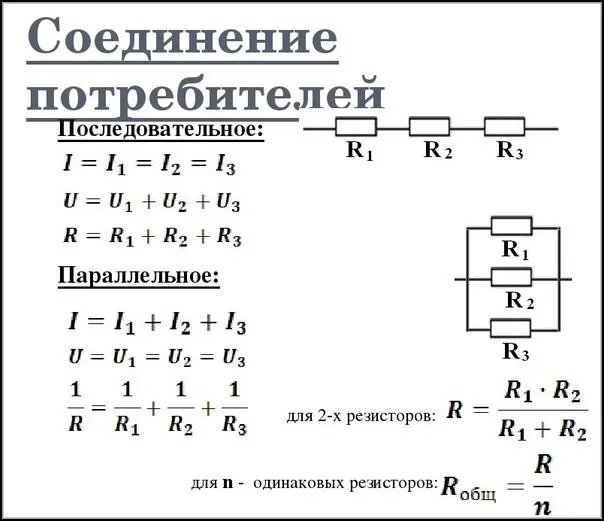
  Типы соединений в электрических схемах

  Основные типы соединений компонентов (потребителей) цепей следующие:

  • Последовательное.
  • Параллельное.
  • Смешанное.

  Первые два типа показаны на рисунке ниже.

  

  Первые два типа показаны в первых двух примерах.

  Очевидно, что смешанный тип соединения представляет собой комбинацию параллельных и последовательных секций.

  

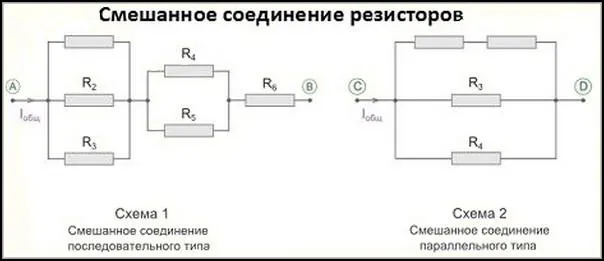
  Алгоритм расчета токов на основе ZO и PC хорошо работает, когда вся цепь состоит из участков со смешанными соединениями с различным количеством нагрузок (сопротивлений). Формулы для участков цепи, показанные на рисунках 03 и 04, просты и удобны для анализа цепи. Однако некоторые схемы не всегда являются таковыми. К ним относятся, например, треугольные и звездообразные сегменты цепи.

  

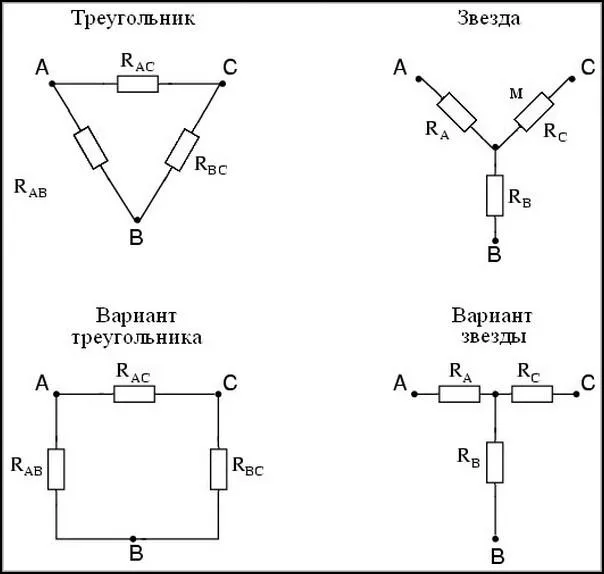
  Следует отметить, что элементы в этих конфигурациях при соединении не считаются исключительно параллельными или последовательными цепями. В англоязычной литературе вместо треугольника используется термин «дельта» и делается ссылка на соответствующую греческую букву D, а звезда обозначается английской буквой Y. В таких случаях очень удобен метод преобразования «электрического» треугольника в звезду (D — Y). Следовательно, возможно и обратное преобразование звезды в соответствующий треугольник (Y в D).

  От треугольника к звезде

  Чаще всего необходимо преобразовать D в Y. Смысл замены заключается в том, что потенциалы трех точек A, B, C и токи, входящие и выходящие из них, должны оставаться неизменными. Поэтому окружающий контур не «почувствует» никаких изменений.

  

  На рисунке выше показаны формулы, которые можно использовать для правильного перехода (обмена) треугольного резистора на эквивалентную звезду (D на Y), или обратно Y на D. Для вывода формул создается система уравнений на базе ПК, где неизвестными являются сопротивления R_A, R_B, R_C(случай от D до Y). Решение системы уравнений получается из значений сопротивлений R_A, R_B, R_Cвыраженное значениями сопротивления в треугольнике R_AВ, R_BС, R_AC.

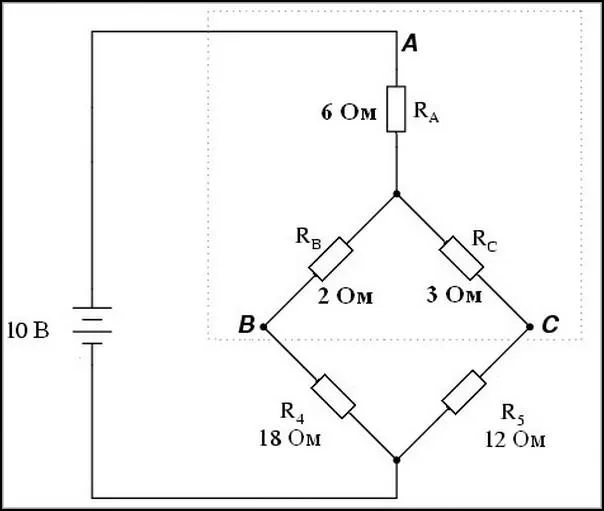
  Если звёзды преобразовывают, то это кому-нибудь нужно

  В качестве примера метода на следующей схеме показана мостовая схема с набором резисторов R.₁, R₂, R₃, R₄, R₅.

  

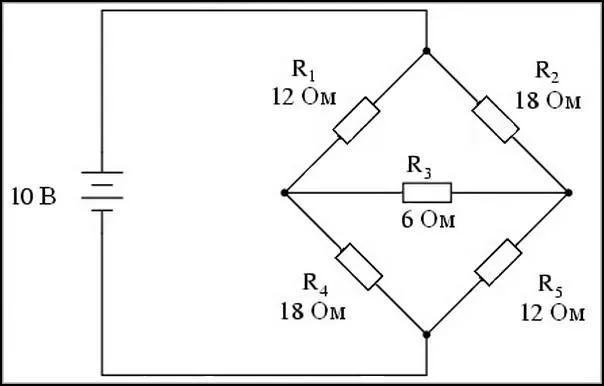
  Для резисторов A, B, C можно использовать упомянутый метод, т.е. преобразование дельты в звезду (D в Y).

  

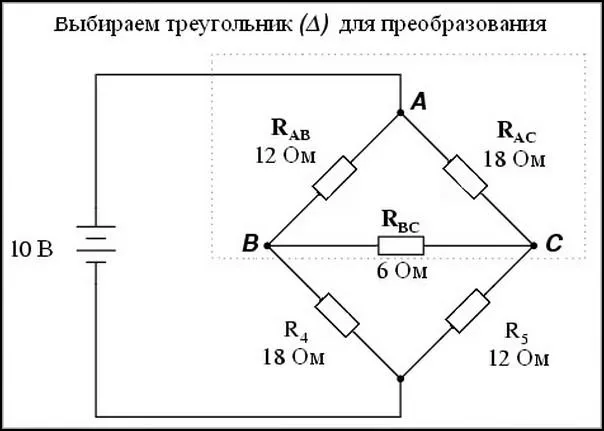
  Используйте формулы для расчета сопротивления звезды R_A, R_B, R_C.

  

  Преобразование треугольника в звезду, таким образом, приводит к схеме, показанной на следующем рисунке.

  

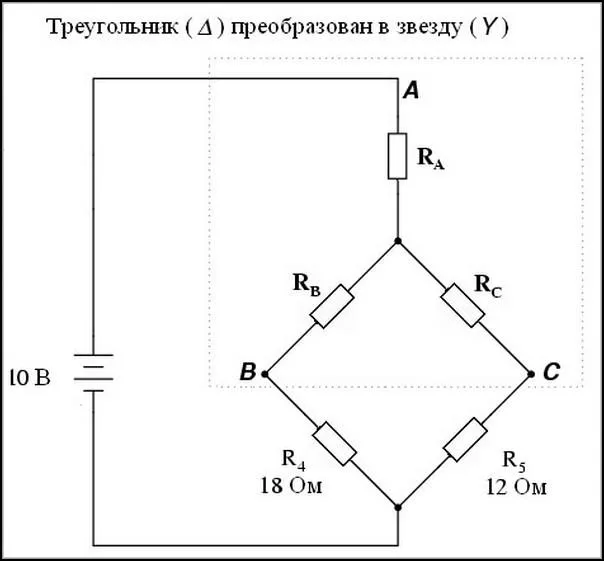
  После замены R_A, R_B, R_Cс ранее рассчитанными числовыми значениями, вы получите простую эквивалентную схему, состоящую только из последовательных и параллельных цепей.