Кроме того, эти величины каким-то образом связаны с угловыми смещениями , угловая скорость; и угловое ускорение. .
Формула угловой скорости
Круговое движение точки вокруг оси — это движение, при котором орбита точки представляет собой окружность, центр которой находится на оси вращения, а плоскость окружности перпендикулярна оси.
Вращение тела вокруг оси — это движение, при котором все части тела совершают круговое движение вокруг этой оси.
Вращательное движение выражается в терминах угла поворота $(ɛ varphi)$. Часто используется базовый вектор вращения $\bar $. Он равен по величине основному углу поворота $(d \ varphi)$ объекта в короткое время dt и ориентирован вдоль мгновенной оси вращения. Направление вращения, по-видимому, против часовой стрелки. Обратите внимание, что только фундаментальное угловое смещение является вектором. Угол поворота при конечных значениях не является вектором.
Угловая скорость — это скорость изменения угла поворота, обычно обозначается буквой $ \omega$. Математически определение угловой скорости записывается следующим образом
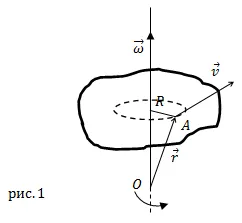
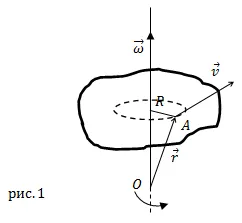
Угловая скорость является векторной величиной (это осевой вектор). Он имеет направление вдоль мгновенной оси вращения, которое совпадает с направлением поступательного правого винта при вращении в направлении вращения тела (рис. 1).
Вектор угловой скорости может быть изменен как путем изменения скорости вращения объекта вокруг своей оси (изменение коэффициента угловой скорости), так и путем поворота оси вращения в пространстве ($ \ бар).<\omega>(тем самым изменяя направление).
Равномерное вращение
Если объект вращается на одинаковый угол и через равные промежутки времени, то такое вращение называется равномерным. В этом случае измеренная угловая скорость равна
где $(ɛ varphi)$ — угол поворота, а t — время, в течение которого происходит этот поворот.
Равномерное вращение часто характеризуется периодом вращения (t). Это время, необходимое для вращения тела ($ \ дельта \ varphi = 2 \ pi $). Угловая скорость связана с периодом вращения следующим образом.
Используя число оборотов в единицу времени ($ \ nu), угловая скорость связана со следующим уравнением
Термины период вращения и обороты в единицу времени иногда используются для описания неравномерного вращения, но подразумевается мгновенное значение T, т.е. время, необходимое объекту для вращения, если он вращается равномерно при заданном мгновенном значении. Скорость.
Формула, связывающая линейную и угловую скорости
Линейная скорость $ \ бар $ точки A (рис. 1) на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением.
где $ \ бар $ перпендикулярно компоненте оси вращения радиус-вектора точки $A (⌘ бар)$ (рис. 1). Вектор $\ bar $ проведен из точки на оси вращения по направлению к этой точке.
Если угловая скорость постоянна, т.е. объект вращается на один и тот же угол и через равные промежутки времени, то говорят, что объект движется равномерно по окружности.
Угловая скорость и угловое ускорение
Рассмотрите понятия угловой скорости и углового ускорения при вращении твердого объекта.
Угловая скорость — это скорость вращения объекта, определяемая увеличением угла поворота объекта за определенный период времени.
Имя: ω (омега).
Виды угловой скорости.
В зависимости от заданных параметров вращения формула для расчета угловой скорости выглядит следующим образом.
- Число оборотов в единицу времени, об/мин, с-1.
- Угол поворота в единицу времени, рад/с.

Скорость изменения угла φ (смещение из положения P).1 Должность P2) — угловая скорость:.
Например, угловая скорость объекта, вращающегося со скоростью 1,5 оборота в секунду, равна
Принимая k за единицу ортов в положительном направлении оси, имеем
Вектор угловых скоростей — это вектор скольжения. Он может быть применен к любой точке на оси вращения и всегда ориентирован вдоль оси. Положительные значения угловой скорости совпадают с направлением ω и k, а отрицательные значения — это Напротив.
Угловое ускорение
Угловое ускорение — это скорость изменения угловой скорости при вращении твердого тела.
Единицы измерения углового ускорения: рад / с 2, с -2.
Векторы углового ускорения также отображаются вдоль оси вращения. При ускоренном вращении они движутся в одном направлении, а при замедлении — в противоположном.
Другими словами, положительное ускорение увеличивает угловую скорость, а отрицательное — замедляет вращение.
Для некоторых особых случаев вращательного движения твердых тел можно использовать следующее уравнение
-
равномерное вращение ( ω — const )
В технике угловая скорость часто указывается в оборотах в минуту nrpm. Один оборот составляет 2π радиуса:.
Уважаемые студенты! На нашем сайте вы можете получить помощь в решении технических и других проблем: ✔ Задачи и решения тестов ✔ εξετά экзамен помощь в изучении конспектов

Решение задач, контрольных и РГР
При необходимости вы можете добавить файлы или фотографии своей работы.
Вы будете проинформированы о цене в течение пяти минут на указанный вами адрес электронной почты.
Если вас устраивает цена, вы можете оформить заказ.
Учебный комплект для студентов.
-Учебный блок A4 -Различные цвета обрамления заметок -Дизайнерский шрифт ГОСТ (государственный стандарт) -Чековые и полосатые листы
Решение. Определите функцию, которая связывает измеренные значения скорости тела и времени (t) ($ \omega(t)$). Векторы $\bar$ и $\bar$ перпендикулярны друг другу, так что
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Продолжительность вращения Земли вокруг Солнца составляет один год или 365 дней. Земля вращается с запада на восток вокруг своей оси, период вращения составляет один день или 24 часа. Широта — это угол между плоскостью экватора и направлением от центра Земли к точке на ее поверхности.
Согласно второму закону Ньютона, сила является причиной любого ускорения. Если движущееся тело испытывает центростремительное ускорение, природа сил, вызывающих это ускорение, может быть различной. Например, если тело движется по кругу на привязанной к нему веревке, то действующая сила — это сила упругости.
Если объект на диске вращается вокруг диска, то сила является силой трения. Когда сила трения перестает действовать, тело продолжает двигаться по прямой линии
Движение по циклоиде*

В системах отсчета, связанных с колесом, точка равномерно вращается по окружности радиуса R со скоростью, которая изменяется только в направлении. Центростремительное ускорение точки направлено к центру окружности по радиусу.
Теперь перейдем к наземным неподвижным системам. Поскольку ускорение не меняется при переходе из одной инерциальной системы отсчета в другую, полное ускорение в точке A остается неизменным как по коэффициенту, так и по направлению. С точки зрения неподвижного наблюдателя, траектория точки A уже не окружность, а более сложная кривая (циклоида), точки которой движутся неравномерно.
Каждая точка окружности движется с определенной скоростью. Эта скорость называется линейной скоростью. Направление вектора линейной скорости всегда совпадает с касательной линией окружности. Например, искра, вылетающая из-под шлифовального круга, движется в том же направлении, что и ее мгновенная скорость.
Равномерное движение тела по окружности
Если угловая скорость постоянна, т.е. объект вращается на один и тот же угол и через равные промежутки времени, то говорят, что объект движется равномерно по окружности.
; — угловая скорость (фиксированная во времени); — угловое смещение t — является ли время поворота углом?
На графике угловой скорости площадь прямоугольника соответствует угловому сдвигу, так что
Постоянная угловая скорость — это отношение углового смещения (угла поворота) к времени, необходимому для этого смещения.
Si единицы угловой скорости:.
Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно увеличивается.
; — мгновенная угловая скорость тела в момент времени t. — Фиксированное угловое ускорение в момент времени t. — Угловое смещение тела в момент времени t (?в радианах) t — время.
На диаграмме скоростей угловой сдвиг равен площади треугольника, так что
Изменение угловой скорости, поскольку вращение тела начинается из состояния покоя. Равна угловой скорости, достигнутой в результате ускорения. Таким образом, этот тип имеет следующий вид
Равномерно ускоренное движение по окружности с начальной угловой скоростью
В момент t = 0; начальная скорость тела, равная 0, изменяется одинаково. (Угловое ускорение постоянно.) ?
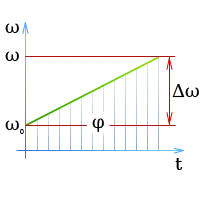
? 0 — начальная угловая скорость. — Существует ли угловая скорость? — Имеет ли место угловое смещение тела в момент времени t в радианах? — Постоянная углового ускорения в момент времени t
На диаграмме скоростей угловой сдвиг соответствует площади таблицы под кривой скорости, поэтому
Поскольку площадь трапеции равна сумме площадей треугольника и прямоугольника, образующих ее, следует, что
Затем возникает график скорости
комбинируя типы, которые мы получаем.
После преобразования получаем уравнение, но оно не содержит времени; — касательная к времени t и касательная к времени t.
; — угол между касательной к оси времени t и осью. — мгновенная угловая скорость; — угловой сдвиг времени t.
Нормальное ускорение
При равномерном круговом движении скорости V и ω остаются неизменными. Меняется только направление вектора скорости.
При таком равномерном круговом движении на тело действует центробежное или нормальное ускорение. Она направлена к его центру по радиусу окружности.
Мера центра ускорения может быть рассчитана по следующим типам
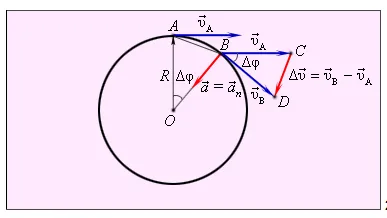
Рассмотрим, как меняется вектор V→ за короткий промежуток времени ΔT. d v→ = v b→ — v a→.
В точках A и B вектор скорости направлен по касательной к окружности, и коэффициент скорости одинаков в обеих точках.
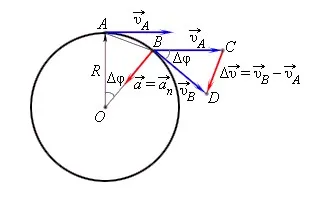
Треугольники OAB и BCD аналогичны. Это выглядит как a a a b = b c c d.
для малых углов δ, расстояние a b = Δs ≈ v — Δt. Для подобных треугольников выше, o a = r и c d = d v, имеем
r v d t = v d v или Δvd t = v 2 r
Если d → 0, то вектор d v → = v b → — v a → адрес, приближающийся к центру центра окружности. Предполагая Δt → 0, получаем
a→= a n→= Δv→Δt; D T→0; a n→= v 2 r.
При равномерном круговом движении измерение ускорения остается стабильным, а направление вектора меняется со временем, сохраняя свою направленность к центру окружности. Поэтому это ускорение называется центробежным ускорением. Вектор в определенный момент времени направлен к центру окружности.
Запись центра векторного ускорения показана ниже.
Здесь — вектор радиуса одной точки окружности, в которой начинается r → центр.
Тангенциальное ускорение
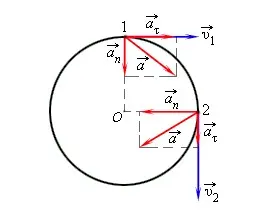
В общем случае, ускорение кругового движения состоит из двух компонентов: нормального ускорения и тангенциального ускорения.
Считайте, что тело рисует круг неравномерно. Ввести понятие тангенциального ускорения. Его адрес совпадает с направлением линейной скорости тела, и в каждой точке цикла он является касательным.
Где d v t = v 2 -v 1 — изменение скорости по горизонтали в пространстве.
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение окружности на одном уровне можно описать с помощью двух координат, x и y. В любой момент времени скорость тела может быть проанализирована на составляющие v x и v y.
Если движение равномерное, то размеры v x и v y и соответствующие координаты изменяются со временем по гармоническому закону длительности t =2πrv = 2 p