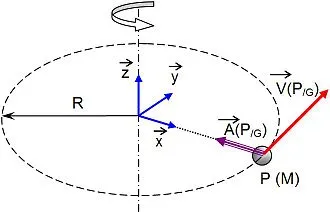
На расстоянии в 152 миллиона километров до Солнца скорость падает до 29,2 км/с. Эта зона называется афелием. Здесь Fцб самая низкая, потому что дистанция до звезды больше, а скорость ниже средней.
Центробежная сила
Центробе́жная си́ла 1 — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.
Зачастую это бывает удобно. Например, когда вращается целиком вся лаборатория, может быть более удобным рассматривать все движения относительно нее, введя лишь дополнительно силы инерции, в том числе центробежную, действующие на все материальные точки, чем учитывать постоянное изменение положения каждой точки относительно инерциальной системы отсчета.
Часто, особенно в технической литературе, во вращающуюся с телом неинерциальную систему отсчёта переходят неявно, и говорят о проявлениях закона инерции как о центробежной силе, действующей со стороны движущегося по круговой траектории тела на вызывающие это вращение связи, и считают её по определению равной по модулю центростремительной силе и всегда направленной в противоположную ей сторону.
Однако в общем случае, когда мгновенный центр поворота тела по дуге окружности, которой аппроксимируется траектория в каждой её точке, может не совпадать с началом вектора силы, вызывающей движение, неверно называть действующую на связь силу силой центробежной. Ведь есть ещё составляющая силы связи, направленная по касательной к траектории, и эта составляющая будет изменять скорость движения тела по ней. Поэтому некоторые физики вообще избегают использовать термин «центробежная сила», как ненужный. 2
Содержание
Обычно понятие центробежной силы используется в рамках классической (Ньютоновской) механики, которой касается основная часть данной статьи (хотя обобщение этого понятия и может быть в некоторых случаях достаточно легко получено для релятивистской механики).
По определению, центробежной силой называется сила инерции (то есть в общем случае — часть полной силы инерции) в неинерциальной системе отсчета, не зависящая от скорости движения материальной точки в этой системе отсчета, а также не зависящая от ускорений (линейных или угловых) самой этой системы отсчета относительно инерциальной системы отсчета.
Для материальной точки центробежная сила выражается формулой:
— центробежная сила приложенная к телу, » width=»» height=»» /> — угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика), — радиус-вектор тела во вращающейся системе координат.
Эквивалентное выражение для центробежной силы можно записать как
» width=»» height=»» />
если использовать обозначение для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
Центробежная сила для тел конечных размеров может быть рассчитана (как это обычно делается и для любых других сил) суммированием центробежных сил, действующих на материальные точки, являющиеся элементами, на которые мы мысленно разбиваем конечное тело.
Вывод
Пусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью а сама система движется поступательно с линейной скоростью в инерциальной системе координат и одновременно вращается с угловой скоростью
Тогда линейная скорость тела в инерциальной системе координат равна:
_n,» width=»» height=»» />
где
\vec v= \frac\vec _0 + \frac\left \vec \omega \times \vec R \right +\frac \vec _n.» width=»» height=»» />
Найдём значение каждого слагаемого в инерциальной системе координат:
\vec _0 = \vec _0 ,» width=»» height=»» />
\vec _n = \vec _n + \left \vec\omega \times \vec _n \right,» width=»» height=»» />
\left \vec\omega \times \vec R \right = \left \vec \varepsilon \times \vec R \right + \left \vec\omega \times \frac \vec R \right = \left \vec \varepsilon \times \vec R \right + \left \vec\omega \times \vec _n \right + \left \vec\omega \times \left \vec\omega \times \vec R \right \right,» width=»» height=»» /> где — угловое ускорение.
\vec v = \vec a=\vec _0 + \vec _n + \left \vec \varepsilon \times \vec R \right + 2\left \vec \omega \times \vec _n \right+ \left \vec \omega \times \left \vec \omega \times \vec R \right \right.» width=»» height=»» />
Последнее слагаемое и будет центростремительным ускорением.
Раскрыв двойное векторное произведение и положив перпендикулярным оси вращения, получим:
В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел, и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.
Различие между центробежной и центростремительной силой
На любой объект, который вращается по круговой траектории, действует сила. Она направлена к центральной точке окружности, описываемой траектории. Такая сила называется центростремительной.
Центробежная сила часто упоминается как сила инерции или фиктивная сила. Она в основном используется для ссылки на силы, которые связаны с движением в неинерциальной системе отсчета.
Согласно третьему закону Ньютона, каждое действие имеет противоположное ему по направлению и равное по силе противодействие. И в этой концепции, центробежная сила является реакцией на действие центростремительной силы.
Обе силы являются инерциальными, так как возникают только при движении объекта. Также они всегда появляются парами и уравновешивают друг друга. Поэтому на практике ими часто можно пренебречь.
Примеры центробежной и центростремительной силы
Если взять камень и привязать к нему веревку, а затем начать вращать веревку над головой, то возникнет центростремительная сила. Она будет действовать через веревку на камень и не позволять ему удаляться на расстояние больше длины самой веревки, как это произошло бы при обычном броске. Центробежная сила будет действовать противоположным образом. Она будет количественно равна и противоположна по направлению центростремительной силе. Такая сила тем больше, чем массивнее тело, движущееся по замкнутой траектории.
Общеизвестно, что Луна вращается вокруг Земли по круговой орбите. Сила притяжения, которая существует между Землей и Луной есть результат действия центростремительной силы. Центробежная сила, в этом случае, является виртуальной и на самом деле не существует. Это вытекает из третьего закона Ньютона. Однако, несмотря на абстрактность, центробежная сила выполняет очень важную роль во взаимодействии двух небесных тел. Благодаря ей Земля и ее спутник не отдаляются и не сближаются друг с другом, а движутся по стационарным орбитам. Без центробежной силы они давно столкнулись бы.
Шар, вращающийся вокруг оси, удерживается пружиной (простая модель веревки). Сила (1) — центробежная сила. Сила (2) центростремительная сила. Она напрягает весну
Выражение центробежной силы
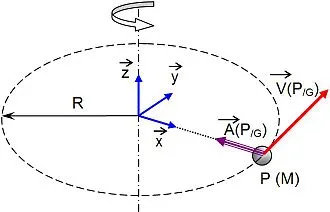
Это напрямую связано с классической кинематикой и тремя законами движения Ньютона . Его интенсивность определяется формулой:
Эти два эквивалентных отношения действительны в Международной системе единиц со следующими обозначениями и единицами ( при необходимости конвертируйте единицы ):
- F cen _ >> центробежная сила в ньютонах (Н), где 1 ньютон близок к 0,1 килограмм-силе;
- m — масса рассматриваемого объекта в килограммах (кг);
- ω — угловая скорость в радианах в секунду (рад / с), поэтому 1 оборот в секунду = 6,28 рад / с и 1 оборот в минуту = 0,105 рад / с;
- v — линейная скорость по касательной к пути в метрах в секунду (м / с), 1 м / с соответствует 3,6 км / ч;
- R — расстояние от оси вращения до центра тяжести объекта, то есть радиус кривизны пути в метрах (м).
Центробежная сила может быть представлена вектором, перпендикулярным мгновенной оси вращения .
Центробежная сила и ускорение
Центробежная сила и вес, действующие на объект массы m, — это две силы, которые пропорциональны m (согласно принципу эквивалентности ). Кроме того, часто бывает более выразительным рассматривать не силы F, а ускорения F / m .
Ускорение — это кинематическая величина, единицей СИ является метр в секунду в квадрате (м / с 2 ).
Также можно использовать число g , определяемое соотношением между рассматриваемым ускорением и ускорением свободного падения , которое составляет приблизительно 9,81 м / с 2 .
Таким образом, на обыденном языке число g составляет десятую часть значения ускорения, выраженного в м / с 2 .
Порядки величины центробежных ускорений
В зависимости от скоростей (линейных или угловых) и радиусов кривизны R численный расчет дает приблизительно см. желаемый :
- 0,1 г : поезд TGV, 360 км / ч , R = 10 км .
- 0,5 г : велосипед наклонен на 26 ° от вертикали, 36 км / ч , R = 20 м .
- 1 г : гипотетическая искусственная гравитация в космической среде, 2 об / мин , R = 224 м .
- 3 г : семена гороха на роторном сортировщике, 366,2 об / мин , R = 2 см
- 5 г : ресурс или поворота пропеллера плоскости , 1 800 км / ч , Р = 5 км ; или винтовой, 180 км / ч , R = 50 м .
- 8 г : ресурс реактивного самолета , 720 км / ч , R = 500 м .
- 13 г : человеческая центрифуга для обучения летчиков-истребителей, 0,64 об / мин , R = 8 м .
- 504 г : отжим белья из стиральной машины, 1400 об / мин , R = 23 см (диаметр барабана = 46 см ).
- 25000 г : лабораторная центрифуга , 15000 об / мин , R = 10,14 см .
- 1000000 g : центрифуга для обогащения урана , 100000 об / мин , R = 9,1 см (гипотетически).
Примеры
Автомобиль в повороте
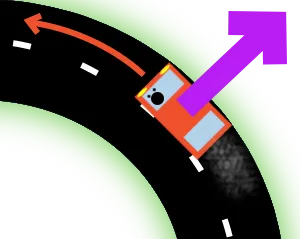
Это неизбежно для вращающихся систем, но может доставлять неудобства пассажирам транспортного средства, меняющим направление движения. Затем они чувствуют центробежную силу, выталкивающую их из поворота. Согласно основному принципу динамики , сиденье втягивает пассажира внутрь, иначе пассажир не повернется вместе с автомобилем. Действительно, это ощущение связано с инерцией (способностью любого материального тела противостоять навязанному движению). Предмет, помещенный на приборную панель, скользит по направлению к внешней стороне автомобиля в повороте, при этом сцепление с приборной панелью оказывается недостаточным, чтобы заставить ее следовать за поворотом; объект фактически уходит прямо (следовательно, наружу для наблюдателя, находящегося в автомобиле). Внешний наблюдатель увидит траекторию, касательную к траектории поворота транспортного средства, а не радиальную траекторию в направлении так называемой центробежной силы.
Для компенсации этого эффекта мы прибегаем к устройствам: комбинация противодействующих перегрузок пилотов истребителей , система наклона некоторых поездов , наклонные повороты дорог, наклон транспортных средств с менее чем четырьмя колесами в поворотах (велосипеды, мотоциклы и двухколесные самокаты, трехколесные самокаты, оснащенные системой гидравлического опрокидывания ).
Отжать белье
Вращательное движение, прикладываемое к белью барабаном стиральной машины, вызывает ускорения, которые также передаются частицам воды. Пока они оставались застрявшими в состоянии покоя, из-за капиллярного воздействия на ткань силы сцепления становятся недостаточными, когда узел вращается достаточно быстро. Локальное равновесие больше не гарантируется, и вода выбрасывается.
Разделение жидкости
Элементы, составляющие гетерогенные жидкости, такие как кровь , разделяются по тому же принципу ультрацентрифугированием . Силовое поле , индуцированное центробежный эффект похоже на более сильное гравитационное поле , которое благоприятствует осаждение из фаз из различных плотностей .
Центробежные регуляторы (на старых паровых машинах)
На схеме ниже воспроизводится принцип работы регулятора Джеймса Ватта . Приводимый машиной через ремень, ротор видит, как его вес удаляется. Затем рычажный механизм управляет клапаном. Воздействие на клапан оказывает обратное влияние на мощность, подаваемую на машину, что позволяет управлять системой. Независимо от того, закрывается ли клапан слишком быстро или слишком медленно, система в конечном итоге находит баланс и, следовательно, регулируемую скорость.