Если говорить о нахождении объема такой геометрической фигуры, то следует отметить, что это задача не только для школьной программы. Используя приведенные выше методы, можно вычислить объем контейнера неизвестного типа.
Формулы, позволяющие находить объём цилиндра в метрах и литрах
Среди множества геометрических фигур также часто встречается цилиндр. Это геометрическое тело используется в многочисленных расчетах. По принятой терминологии под таким понятием принято понимать тело геометрического типа, имеющее в своей основе поверхность. Эта поверхность также имеет цилиндрическую форму.
В литературе эту поверхность часто называют поверхностью бокового обзора. Также на такой фигуре есть пара поверхностей, называемых основаниями. Основания этих цилиндров представляют собой круги одинакового диаметра. Цилиндр, в основании которого находится круг, считается круглым.
Со школьных времен всем знакома фигура цилиндра классического типа. Это круговой цилиндр.
Типы цилиндров
В математике есть несколько типов цилиндров, которые постоянно используются в геометрии.
- Прямой цилиндр. Это геометрическая фигура, имеющая прямой угол между боковой поверхностью и основаниями. Этот тип является наиболее распространенным и часто используется для решения большого количества задач.
- Цилиндр наклона. Исходя из основания фигуры, можно сделать вывод, что угол между боковой поверхностью и основаниями фигуры будет отличаться от прямого. При этом он может колебаться в своем значении, как вверх, так и вниз от прямого угла.
— геометрическое тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями (основаниями). Цилиндр называется круглым, если его основание представляет собой окружность. Расстояние между основаниями равно высоте цилиндра.
Объем цилиндрической полости
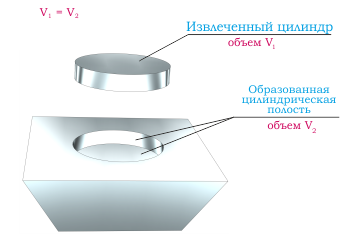
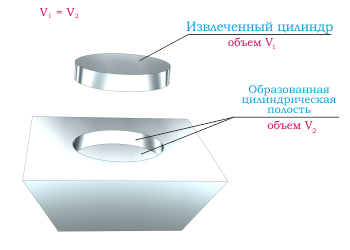
Объем цилиндрической полости равен объему цилиндра, вытянутого из этой полости для ее образования. То есть для расчета цилиндрической полости можно использовать формулы и калькулятор для расчета простого регулярного цилиндра, исходя из известных исходных данных.
На изображении показана цилиндрическая полость, образовавшаяся в корпусе при удалении цилиндра. Объем извлеченного цилиндра и объем образовавшейся полости равны.
Следует отметить важный момент. Несмотря на равенство объемов извлекаемого цилиндра и образовавшейся полости, площади поверхностей этих объектов будут различны, так как сформированная цилиндрическая полость не имеет верхней поверхности. То есть общая площадь поверхности образовавшейся цилиндрической полости будет меньше общей площади удаляемого цилиндра на площадь основания цилиндра.
Правильный цилиндр — это цилиндр, у которого угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильным или наклонным цилиндром называется цилиндр, у которого угол между образующими боковой поверхности и основанием цилиндра отличен от 90 градусов.
Рассмотрим обычный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя окружностями, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно также описать как тело, состоящее из двух равных окружностей, расположенных не в одной плоскости и параллельных друг другу, и отрезков, соединяющих все точки одной окружности с соответствующими точками другой окружности. Эти сегменты называются цилиндрообразующими.
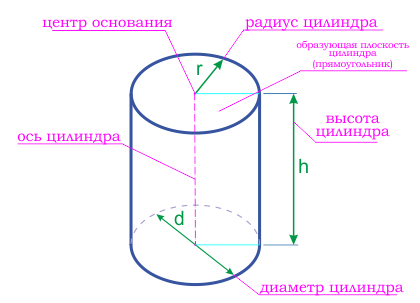
Радиус основания цилиндра — это радиус цилиндра.
Ось цилиндра представляет собой прямую линию, соединяющую центры оснований цилиндра.
Высота цилиндра — это перпендикуляр, проведенный от одного основания цилиндра к другому.
Поверхности цилиндра
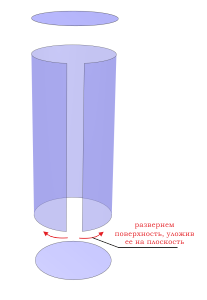
Внешнюю поверхность цилиндра можно условно разделить на три отдельные поверхности: верхнюю, нижнюю и боковую.
Верхняя и нижняя поверхности цилиндра круглые и равные.
Боковая поверхность цилиндра имеет форму прямоугольника. Для наглядности возьмем наружную боковую поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Затем преобразуйте поверхность в плоскость. В результате мы увидим, что боковая поверхность имеет форму прямоугольника (см изображение).
Следует отметить, что параметры горизонтальных, наклонных, косых, круглых и равносторонних полых цилиндров рассчитываются по дополнительным формулам.
Нахождение объема цилиндра: формула и задачи
В этом посте мы увидим, как можно найти объем цилиндра, и обсудим примеры решения задач.
Через площадь основания и высоту
Объем (V) цилиндра равен произведению его высоты на площадь его основания.
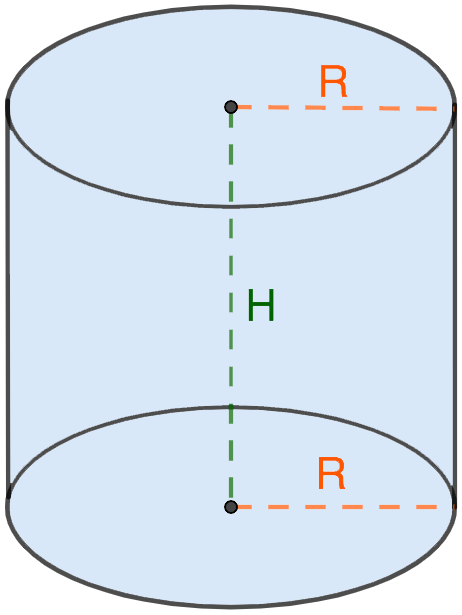
Через радиус основания и высоту
Как известно, основания цилиндра (равные друг другу) представляют собой окружность, площадь которой вычисляется следующим образом: S = π ⋅ R 2 . Следовательно, формулу расчета объема цилиндра можно представляться как:
V знак равно π ⋅ R 2 ⋅ Н
Примечание: при расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как известно, диаметр окружности равен двум ее радиусам: d = 2R. Таким образом, вы можете рассчитать объем цилиндра следующим образом:
Примеры задач
Упражнение 1
Найдите объем цилиндра, если дана площадь его основания: 78,5 см 2 и, кроме того, высота равна 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задача 2
Высота цилиндра 6 см, диаметр 8 см. Найдите объем фигуры.
Решение:
Используя третью формулу, в которую вмешивается диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
На изображении показана цилиндрическая полость, образовавшаяся в корпусе при удалении цилиндра. Объем извлеченного цилиндра и объем образовавшейся полости равны.
Калькулятор объема цилиндра в м3
Цилиндр – это трехмерное тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями. Цилиндр (от греческого «кулиндрос» — каток, каток) относится к основным геометрическим фигурам. В элементарных математических интерпретациях он определяется как трехмерное тело. Объем баллона – один из основных параметров, который необходимо уметь рассчитать каждому человеку. Формула используется во многих областях промышленности, таких как строительство, архитектура, механика и программирование.

Узнать объем пустотелой фигуры можно моментально с помощью удобной онлайн-программы. Сервис позволяет рассчитать параметры тела за секунды и получить результаты в кубических сантиметрах, метрах, литрах. Расчет ведется по двум математическим формулам:
Высота и радиус: V = S x h.
Где V — объем, S — площадь, h — высота. Для расчета объема нужно площадь основания тела умножить на h. Следовательно, для этого должны быть известны две переменные.
R — радиус в квадрате. От первой формулы расчет отличается тем, что сначала нужно найти значение радиуса. Для этого разделите диаметр на 2 или используйте формулу S/2 x ∏ x H. ∏ — константа 3,14 (отношение длины окружности к диаметру).
Объём цилиндра через площадь основания и высоту
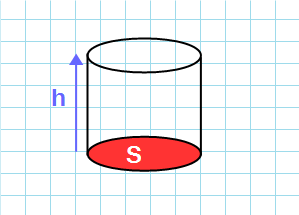
Программа позволяет определить объем тела по обеим формулам. Для этого нужно просто подставить числа в соответствующие строки и нажать кнопку рассчитать. Пошаговая инструкция расчета основных показателей фигуры на калькуляторе по высоте и радиусу:
- в графу «h» введите длину данной фигуры, рядом выберите метрику, в миллиметрах, сантиметрах, метрах;
- в строке «r» введите радиус тела и выберите измерение длины (мм, см, м);
- в столбце «Результат» определите, в каком V он будет отображаться: ведра, литры.
Например, длина фигуры 1,6 метра, радиус 25 сантиметров. Объем 314,2 литра, 314200 куб см или 0,314 куб. М. Результат отображается моментально, с точностью до тысячной. Точность расчета зависит исключительно от достоверности исходных данных.
Где применяется программа
Сервис предназначен для всех пользователей, чья профессиональная деятельность связана с решением математических задач. Калькулятор будет полезен школьникам 5-9 классов, ученикам 11 классов в процессе подготовки к ЕГЭ и контрольным срезам, а также родителям для проверки правильности решения задач.
С помощью сервиса можно решать типовые тестовые задачи из школьной программы, подставляя известные значения и не забывая задавать метрические параметры (в кубических сантиметрах, кубических метрах, миллиметрах, литрах). Например:
Дан цилиндр, площадью основания 58,3 см 2 и высотой 7 см, для расчета V необходимо использовать расчет по площади и высоте.
Решение: V = 58,3 см 2 х 7 см = 408,1 см³ или 0,408 л.
Расчет: Перед использованием программы необходимо определить радиус основания — 16 см / 2 = 8 см. Затем подставить значения в нужные поля. Расчет производится по формуле V = 3,14 х 8 2 х 11 см = 2211,968 см³.
Следует отметить, что параметры горизонтальных, наклонных, косых, круглых и равносторонних полых цилиндров рассчитываются по дополнительным формулам.
Если говорить о нахождении объема такой геометрической фигуры, то следует отметить, что это задача не только для школьной программы. Используя приведенные выше методы, можно вычислить объем контейнера неизвестного типа.
Примеры задач
Упражнение 1
Найдите объем цилиндра, если дана площадь его основания: 78,5 см 2 и, кроме того, высота равна 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задача 2
Высота цилиндра 6 см, диаметр 8 см. Найдите объем фигуры.
Решение:
Используя третью формулу, в которую вмешивается диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Поэтапный расчет объема картонной коробки
- Измерьте длину а и ширину b, если дно коробки квадратное, то a = b;
- Измерьте высоту h как расстояние от дна до верхней створки коробки.
Предварительно необходимо рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5-10 мм меньше внутренних размеров гофроупаковки.
В=а*б*ч
где а — длина основания (м), b — ширина основания (м),
h – высота ящика (м).
Если в основании коробки не прямоугольник, а треугольник, пятерка или шестиугольник, то формула расчета объема будет такой:
В=С*ч
где S — площадь основания ящика, а h — его высота.
Объем, занимаемый заготовкой (коробкой), рассчитывается (с учетом толщины стенки) для ее правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=квадрат (S) * толщина листа
* как рассчитать площадь (S) картонной коробки — в этой статье
| Один тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | Б | 3 |
| Трехслойный гофрокартон | С | 3,7 |
| Трехслойный гофрокартон | Мне | 1,6 |
| Пятислойный гофрокартон | До нашей эры | 7 |
| Пятислойный гофрокартон | БЫТЬ | 4 |
Боковая поверхность цилиндра имеет форму прямоугольника. Для наглядности возьмем наружную боковую поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Затем преобразуйте поверхность в плоскость. В результате мы увидим, что боковая поверхность имеет форму прямоугольника (см изображение).
Найти объем цилиндра
Выберите известные количества:
Ввод данных в калькулятор для вычисления объема цилиндра
Вы можете ввести числа или дроби в онлайн-калькуляторе. Подробнее читайте в правилах ввода чисел.
NB В онлайн-калькуляторе можно использовать значения в одних и тех же единицах!
Если у вас возникли проблемы с преобразованием единиц измерения, используйте конвертер единиц расстояния и длины, конвертер единиц площади и конвертер единиц объема.
Дополнительные возможности калькулятора для вычисления объема цилиндра
Теория. Объем цилиндра.

— геометрическое тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями (основаниями). Цилиндр называется круглым, если его основание представляет собой окружность. Расстояние между основаниями равно высоте цилиндра.
Формулы для вычисления объема цилиндра
где V — объем цилиндра,
Такова площадь основания цилиндра,
R — радиус основания цилиндра,
h — высота цилиндра,
π = 3,141592.
Вы можете вводить числа или дроби (-2,4, 5/7, .). Подробнее читайте в правилах ввода чисел.
Например, длина фигуры 1,6 метра, радиус 25 сантиметров. Объем 314,2 литра, 314200 куб см или 0,314 куб. М. Результат отображается моментально, с точностью до тысячной. Точность расчета зависит исключительно от достоверности исходных данных.
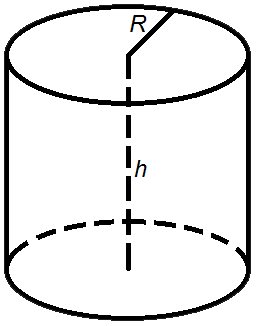
Формула объема цилиндра через диаметр
К сожалению, бывает, что при расчете объема фигуры известны не все размеры. Так, например, может отсутствовать радиоданные.
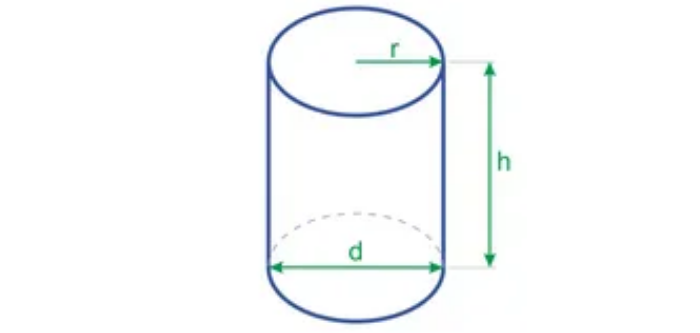
В этом случае, если вы знаете диаметр или можете его измерить, вы можете воспользоваться следующей формулой:
Примеры задач с решениями
Задача №1
Высота бочки с водой 3 метра, радиус 0,75 метра. Вычислите в литрах, сколько жидкости нужно, чтобы заполнить емкость наполовину?
Задача №2
Заготовка цилиндра была изготовлена в цеху. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.
Задача №3
На производстве нужно сделать две трубы с двумя равными поверхностями. Внешний радиус первой трубы 5 см, внутренний радиус 4 см, высота 200 см, внутренний радиус второй 3 см.
Сколько материала нужно для изготовления труб?