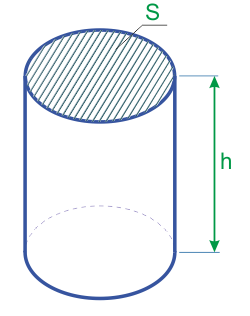
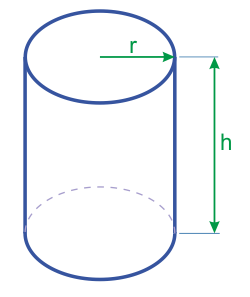
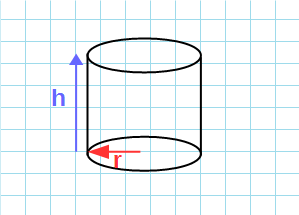
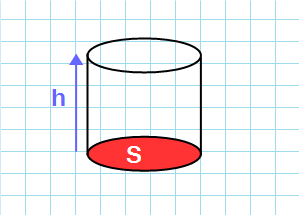
Цилиндр – это объемная геометрическая фигура с параллельными круглыми основаниями. Если вам нужно узнать объем цилиндра, найдите его высоту (h) и радиус основания (r) и подставьте их в формулу: V = hπr 2 .
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
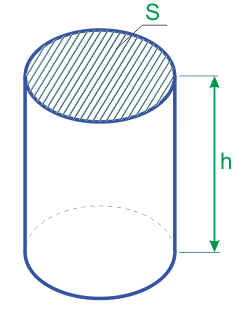
Объем цилиндрической полости
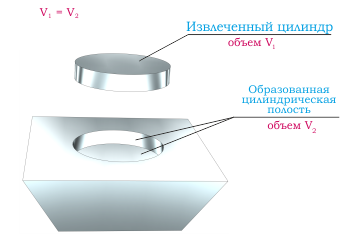
Объем цилиндрической полости равен объему цилиндра, вытянутого из этой полости для ее образования. То есть для расчета цилиндрической полости можно использовать формулы и калькулятор для расчета простого регулярного цилиндра, исходя из известных исходных данных.
На изображении показана цилиндрическая полость, образовавшаяся в корпусе при удалении цилиндра. Объем извлеченного цилиндра и объем образовавшейся полости равны.
Следует отметить важный момент. Несмотря на равенство объемов извлекаемого цилиндра и образовавшейся полости, площади поверхностей этих объектов будут различны, так как сформированная цилиндрическая полость не имеет верхней поверхности. То есть общая площадь поверхности образовавшейся цилиндрической полости будет меньше общей площади удаляемого цилиндра на площадь основания цилиндра.
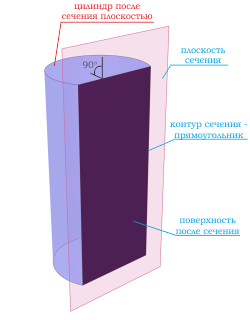
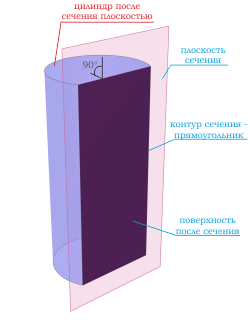
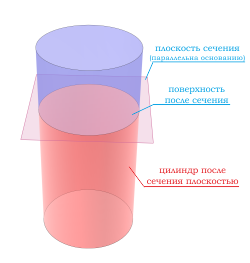
Правильный цилиндр — это цилиндр, у которого угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
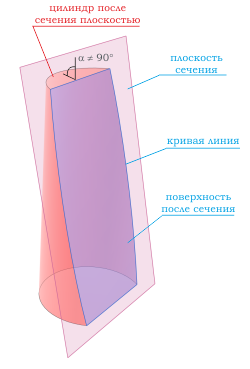
Неправильным или наклонным цилиндром называется цилиндр, у которого угол между образующими боковой поверхности и основанием цилиндра отличен от 90 градусов.
Рассмотрим обычный цилиндр.
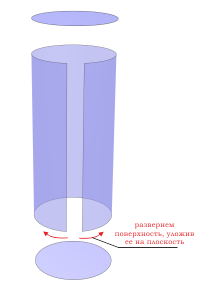
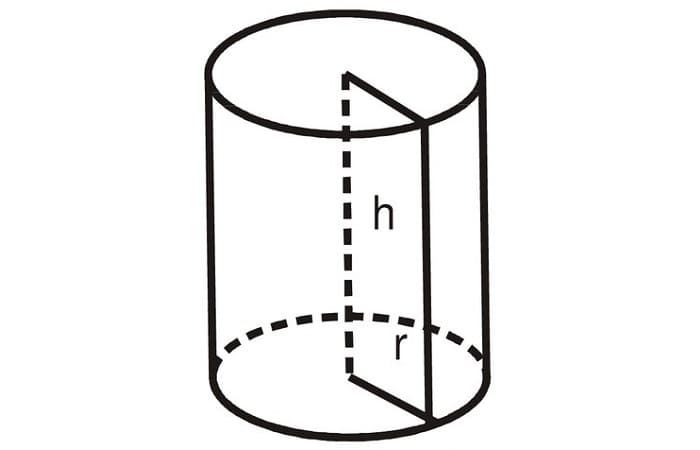
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя окружностями, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно также описать как тело, состоящее из двух равных окружностей, расположенных не в одной плоскости и параллельных друг другу, и отрезков, соединяющих все точки одной окружности с соответствующими точками другой окружности. Эти сегменты называются цилиндрообразующими.
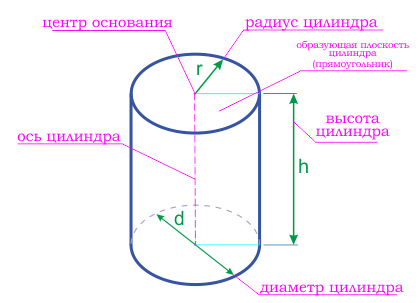
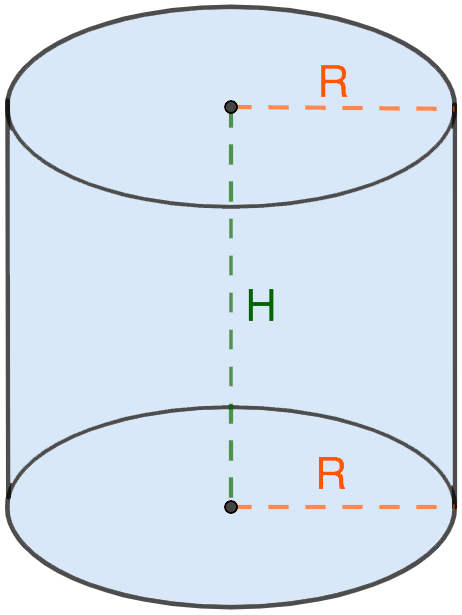
Радиус основания цилиндра — это радиус цилиндра.
Ось цилиндра представляет собой прямую линию, соединяющую центры оснований цилиндра.
Высота цилиндра — это перпендикуляр, проведенный от одного основания цилиндра к другому.
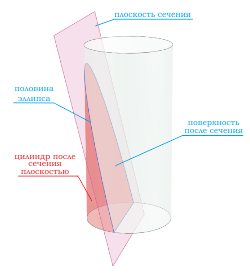
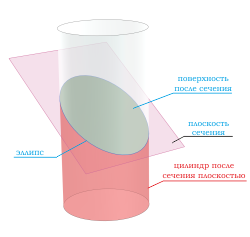
Если секущая поверхность проходит через боковую поверхность, но не параллельна основанию цилиндра, то в сечении получается эллипс .
Как найти объем цилиндра
При упоминании цилиндра на ум приходит классический головной убор. Помимо него, в окружающей среде можно найти множество разновидностей этой фигуры.
Теоретически это тело, ограниченное цилиндрической поверхностью и пересекающимися параллельными плоскостями.
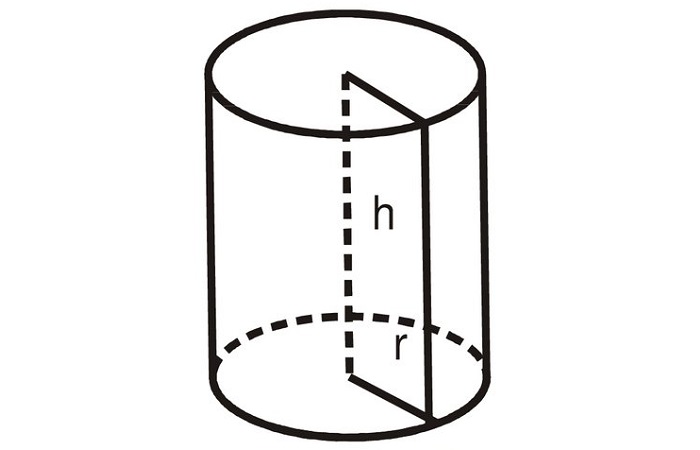
Его объем можно рассчитать следующим образом:
Как видите, формула проста и прозрачна, и если неспециалисту нужно, как вариант, определить объем емкости для воды, он может смело ею пользоваться. Хотя, если есть сомнения в правильности расчетов, можно воспользоваться для этих целей калькулятором и определить объем онлайн.
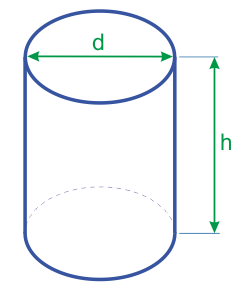
Формула объема цилиндра через диаметр
К сожалению, бывает, что при расчете объема фигуры известны не все размеры. Так, например, может отсутствовать радиоданные.
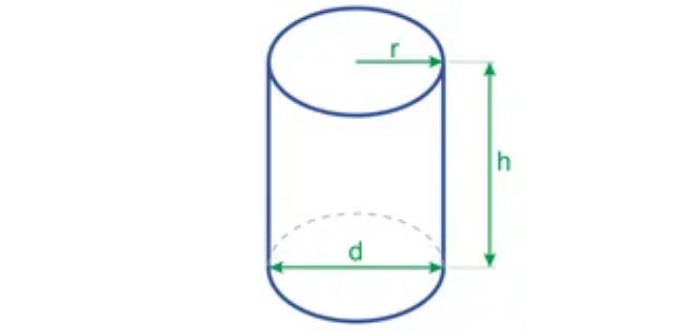
В этом случае, если вы знаете диаметр или можете его измерить, вы можете воспользоваться следующей формулой:
Видно, что в развернутом виде боковая поверхность представляет собой обычный прямоугольник, стороны которого равны высоте и длине окружности основания. Последний факт позволяет записать формулу площади Sb этой фигуры:
Формула объема цилиндра через диаметр
К сожалению, бывает, что при расчете объема фигуры известны не все размеры. Так, например, может отсутствовать радиоданные.
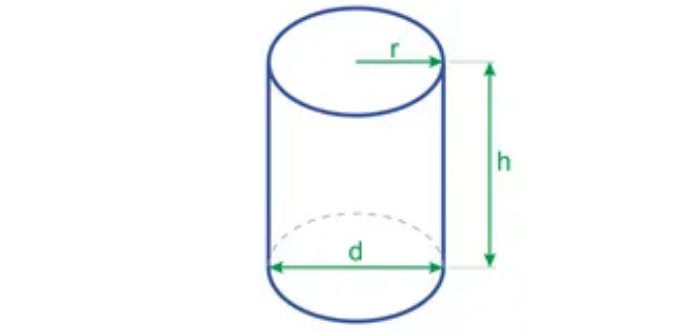
В этом случае, если вы знаете диаметр или можете его измерить, вы можете воспользоваться следующей формулой:
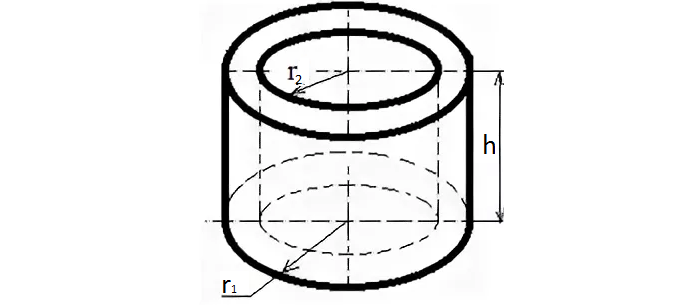
Объем полого цилиндра
Расчет полого цилиндра необходим, когда необходимо, например, рассчитать вес полой трубы. Его масса равна произведению плотности материала на объем.
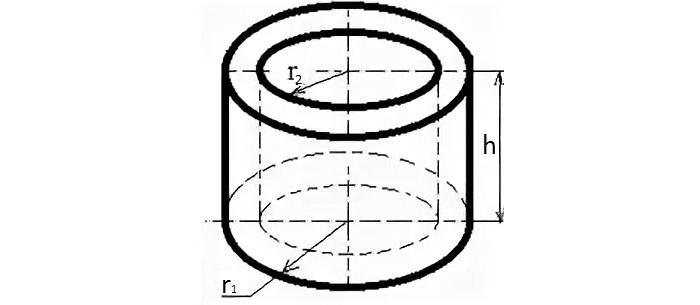
На производстве нужно сделать две трубы с двумя равными поверхностями. Внешний радиус первой трубы 5 см, внутренний радиус 4 см, высота 200 см, внутренний радиус второй 3 см.
Задача на расчет объема цилиндра через площадь его полной поверхности
Предположим, цилиндр имеет высоту 21 см и его развернутую площадь 335 см2. Необходимо определить объем фигуры.
Ни одна из приведенных выше формул не способна дать нам желаемый ответ. Как в этом случае рассчитать объем цилиндра? Как было сказано выше, достаточно знать любые два параметра фигуры, чтобы определить значение V. В этом случае сначала запишем формулу полной площади цилиндра:
S = Sb + 2 * So = 2 * pi * r * h + 2 * pi * r2
Подставляя в это равенство известные данные, получаем:
После подстановки данных делим левую и правую части на 2*пи и переводим все члены в равную часть.
Поэтому перед нами стоит задача решить квадратное уравнение. Используем стандартный метод разрешения через дискриминант, имеем:
При решении уравнения отбрасываем отрицательный корень.
Теперь для определения объема цилиндра можно воспользоваться формулой с параметрами r и h. Подставляя их в указанную формулу, приходим к ответу задачи: V = 345,8 см3.
Видно, что в развернутом виде боковая поверхность представляет собой обычный прямоугольник, стороны которого равны высоте и длине окружности основания. Последний факт позволяет записать формулу площади Sb этой фигуры:
Дополнительные статьи

Об этой статье
wikiHow — это вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали 38 человек, в том числе анонимно. Количество просмотров этой статьи: 68 104.
Файлы cookie помогают улучшить WikiHow. Продолжая использовать наш сайт, вы соглашаетесь с нашей политикой в отношении файлов cookie.