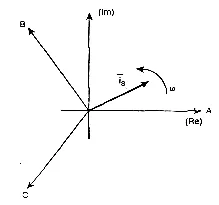
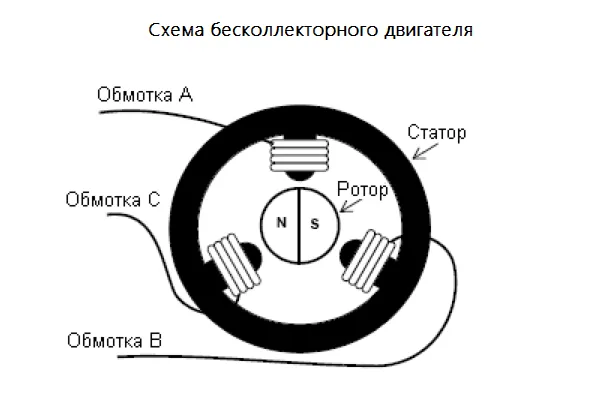
где iq— фазный ток q; aq— угол, измеренный от оси фазной обмотки в направлении, считающемся положительным; KB= const,
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ И МОДЕЛИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ В УСТАНОВИВШИХСЯ И ПЕРЕХОДНЫХ РЕЖИМАХ
Имея математическое описание процессов работы асинхронного двигателя в статическом и динамическом состояниях, можно определить временные зависимости токов статора и ротора, определить потери в асинхронной машине, проанализировать возможность их снижения с помощью энергосберегающих алгоритмов управления электроприводом в переходных и установившихся режимах, выбрать эффективные методы и законы управления асинхронным двигателем в зависимости от потребляемой мощности.
Дифференциальные уравнения обобщенного двухфазного двигателя переменного тока обычно используются для математического описания процессов в асинхронном двигателе 32, 33, 71, полученных при обычных допущениях (игнорирование потерь в стали, высших гармоник магнитного поля в однородном воздушном зазоре и напряжения питания, являющегося симметричной синусоидальной системой напряжения). Также предполагается, что параметры цепи ротора сводятся к параметрам цепи статора.
Исходные уравнения, записанные с помощью обобщенных пространственных векторов в системе координат, вращающейся с произвольной скоростью shk (при отсутствии внешних источников напряжения в цепях ротора), имеют следующий вид:
где Ux — обобщенный вектор напряжения статора; /ь /2 — обобщенные векторы тока статора и ротора, соответственно; RUR2 — активное сопротивление обмоток статора и ротора, соответственно; ðь j/2 — обобщенные векторы коэффициентов цепи статора и ротора, соответственно; сок — электрическая угловая скорость вращения координатных осей; соэ — электрическая угловая скорость ротора,
где w — механическая угловая скорость ротора; M — электромагнитный момент, развиваемый двигателем; pn — число пар полюсов асинхронного двигателя; L0 — индуктивность намагничивающего контура; Jm — знак, указывающий, что берется только вещественная часть комплекса.
Для изучения переходных явлений система уравнений
(1.3) и уравнение (1.4) дополняются уравнением движения электропривода
где Ms — статический момент нагрузки, J — полный момент инерции двигателя, приведенный к валу, /= /dv + /meh- /dv и /meh — момент инерции двигателя, приведенный к валу двигателя, и момент инерции механизма.
Система уравнений (1.3), записанная проекциями обобщенных векторов на ортогональные оси и, jv координатной плоскости, вращающейся с произвольной скоростью сок, имеет следующий вид:
О = R2i2u + p|/2« — (сок -(o3)|/2t,; 0 = R2i2v +PV2v+ (а>к ~ e)X|/2″
где p — оператор дифференцирования.
В этом случае электромагнитный момент, развиваемый асинхронным двигателем, может быть определен из следующего выражения
M — — Pn^o (huhv ~ хув)-
Рациональное значение сок зависит от характера решаемой задачи и обычно принимает одно из следующих значений: шк = О (в этом случае допустимо обозначать координатные оси a, y’P); сок = (о0е (координатные оси x, jy) сок = сое (координатные оси d, jq), где со0е — угловая электрическая скорость электромагнитного поля статора. Это значение соответствует электрической скорости без нагрузки. Обратите внимание, что механическая угловая скорость без нагрузки, синхронная скорость, равна co0 = shoe/rn.
Когда мы обозначаем угловую скорость через co и измеряем ее через c-1, термин «угол» часто опускается и используется термин «скорость».
Связь между общим током статора j/b, током ротора j/2, основным током j/0 и токами статора ix и ротора /2 ненасыщенной асинхронной машины следующая:
ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД
Как показано в подразделе 4.2.7, использование частотно-регулируемых приводов в сочетании с системой управления на основе современных компонентов может привести к значительной экономии энергии в дуговых печах. …
В последнее время наблюдается тенденция использования асинхронных двигателей с переменной частотой в конвейерных системах. Рассмотрим основные преимущества перехода на частотное управление на примере контейнерного козлового крана ККК20-25-8,5-5 грузоподъемностью 20 …
ЭФФЕКТИВНОСТЬ ИСПОЛЬЗОВАНИЯ ЧАСТОТНОРЕГУЛИРУЕМЫХ ЭЛЕКТРОПРИВОДОВ В УСТРОЙСТВАХ НА ПРОМЫШЛЕННЫХ ОБЪЕКТАХ
5.3.1 Поршневые насосы и компрессоры Объектом модернизации является воздушная компрессорная станция для снабжения различных объектов очищенным сжатым воздухом под давлением 7,8 атм. Компрессорная станция состоит из шести компрессоров с…
Контакт для заказов оборудования для производства бетонных блоков: +38 096 992 9559 Инна (вайбер, ватсап, телеграмм) Email: inna@msd.com.u
Метод пространственного вектора
Для упрощения математического описания асинхронной машины, как и всех машин переменного тока в целом, пространственно-векторный метод оказался удивительно удачным и элегантным; он позволил упростить и сократить приведенную выше систему уравнений; метод позволяет связать уравнения (3.1-3.4) в единую систему с векторными переменными состояния. Суть метода заключается в том, что мгновенные значения симметричных трехфазных переменных состояния (напряжения, токи, токи-токи) могут быть математически преобразованы таким образом, чтобы их можно было представить одним пространственным вектором. Это математическое преобразование имеет вид (например, для тока статора):
где — векторы, учитывающие пространственное смещение обмоток, — симметричная трехфазная система тока статора.
Подстановка мгновенных значений токов в уравнение (3.5) дает математическое описание вектора тока в пространстве статора:
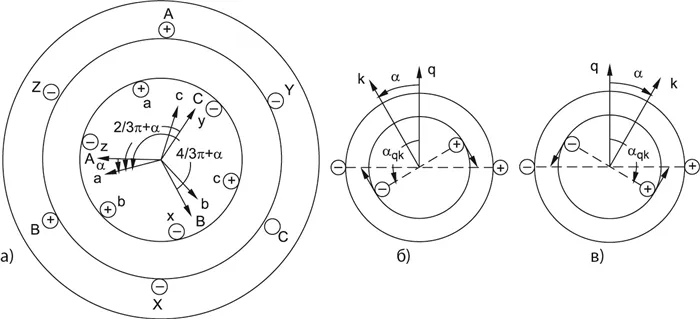
На рис. 3.1 представлена геометрическая интерпретация вектора пространственного тока — это вектор в комплексной плоскости с единицей (длиной) Imс угловой скоростью, вращающейся в положительном направлении. Проекции вектора на оси фаз A, B, C определяют мгновенные токи в фазах. Аналогично, все напряжения, токи и токи цепи уравнений (3.1), (3.2) могут быть представлены пространственными векторами.
Теперь мы можем приступить к упрощению уравнений.
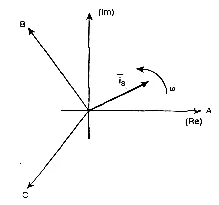
Рис. 3.1 — Вектор космического тока
Шаг первый. Чтобы преобразовать уравнения (3.1) в мгновенные значения в уравнениях в пространственных векторах, умножим их на выражения: первое уравнение на, второе уравнение на, третье уравнение на, — и сложим их отдельно для статора и ротора. Тогда мы получаем
где LS, LR— индуктивности статора и ротора, Lm() — взаимная индуктивность между статором и ротором. Таким образом, вместо двенадцати уравнений (3.1)-(3.2) мы имеем только четыре уравнения (3.7).
Второй шаг. Переменные коэффициенты взаимной индуктивности в уравнениях взаимной индуктивности (3.7) являются следствием того, что уравнения равновесия ЭЭД для статора были записаны в фиксированной системе координат относительно статора, а уравнения равновесия ЭЭД для ротора были записаны во вращающейся системе координат относительно ротора. Используя метод пространственных векторов, эти уравнения можно записать в единой системе координат, вращающейся с любой скоростью.к. В этом случае уравнения (3.7) преобразуются в вид:
где = p*m, p — число пар полюсов в машине.
В уравнении (3.8) все коэффициенты постоянны, имеют ясный физический смысл и могут быть определены из технического паспорта двигателя или экспериментально.
Третий шаг. Этот шаг относится к определению крутящего момента. Импульс в уравнении (3.4) является векторным произведением любой пары векторов. Уравнение (3.8) показывает, что таких пар может быть шесть. В этом случае существует еще четыре способа представления электромагнитного момента машины с помощью следующих пар: Как только выбрана определенная пара, уравнение импульса фиксируется, и число уравнений в системе (3.8) сокращается до двух. Кроме того, в уравнениях (3.3) и (3.4) векторные значения импульса и скорости можно заменить на их модульные значения. Это является следствием того, что пространственные векторы потоков и течений также лежат в плоскости, перпендикулярной оси вращения, а векторы импульса и угловой скорости совпадают с осью. Например, обозначение уравнений импульса по определенным парам переменных состояния машины имеет вид:
Математическая модель асинхронной машины в осях, вращающихся с произвольной скоростью
Уравнения индукционной машины с короткозамкнутой клеткой или машины с фазной обмоткой при отсутствии напряжения питания могут быть получены из уравнений (3.10) путем подстановки.
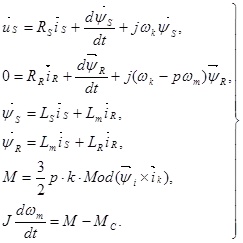
Для динамических систем необходимо учитывать переходные электромагнитные процессы в машине. В этом случае, если сохранить пространственные векторы совпадения токов статора и ротора () как пару переменных, описывающих машину, то уравнения (3.11) после соответствующих преобразований принимают вид, учитывающий уравнения для совпадения токов (3.8):
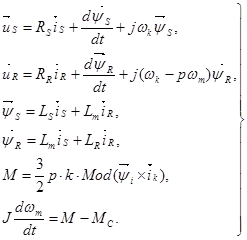
Математическая модель асинхронной машины в неподвижной системе координат
Чтобы лучше понять физические процессы в асинхронной машине, мы рассматриваем машину в фиксированной системе координат.
В фиксированной комплексной системе координат () действительная ось обозначается через, а мнимая — через. Пространственные векторы в этом случае разрешаются вдоль осей:
. Если подставить эти значения в уравнение (3.12) и приравнять отдельно действительную и мнимую части, то получим :
Цифровая модель асинхронного двигателя
Полученная математическая модель АД является существенно нелинейной, что не позволяет аналитически решить ее дифференциальные уравнения, за исключением некоторых случаев. Поэтому для изучения процессов в АД в Mathlab Simulink построена численная модель АД. 3. Блок-схема подсистемы показана на рис. 3. 4.
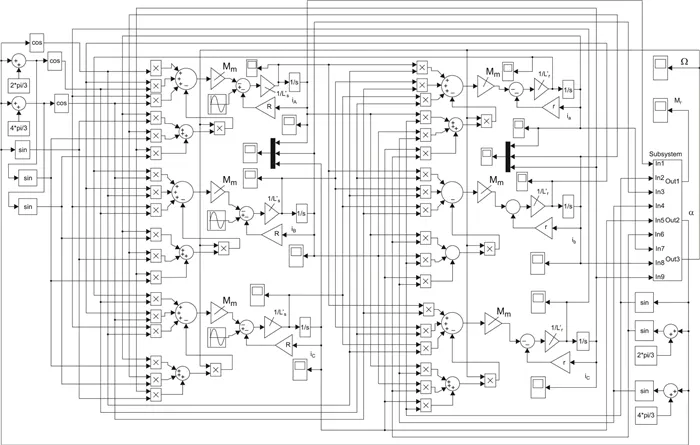
Рисунок 3. Цифровая модель AD
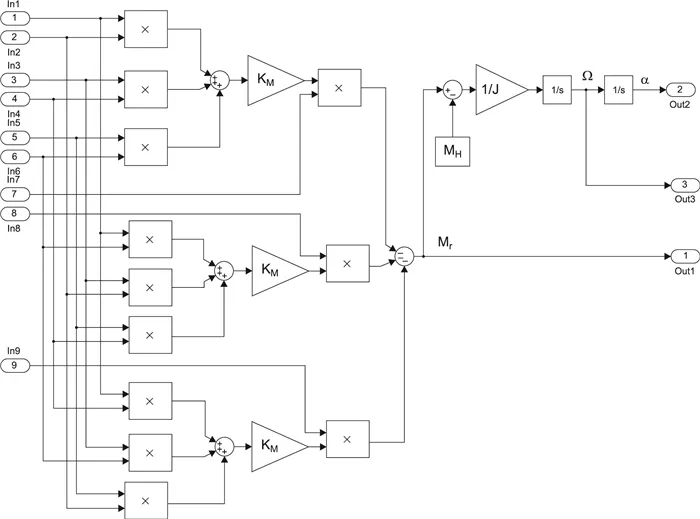
Рисунок 4. Блок-схема подсистемы
Чтобы оценить правильность численной модели, желательно иметь аналитическое решение дифференциальных уравнений, по крайней мере, для конкретного случая. Это относится к тормозному двигателю. Электромагнитные процессы описываются здесь системой линейных дифференциальных уравнений. Переход к образам Лапласа при начальных условиях нуля и трехфазной системы напряжений приводит их к виду (35), где Ik, Uq— изображения Лапласа ik, k = A, B, C, a, b, c и uq, q = A, B, C ,
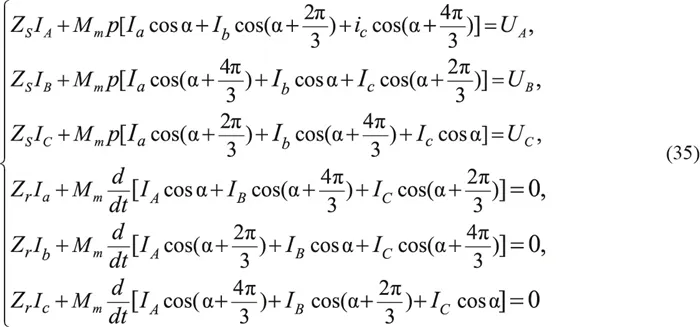
Система линейных уравнений (35) имеет решение:
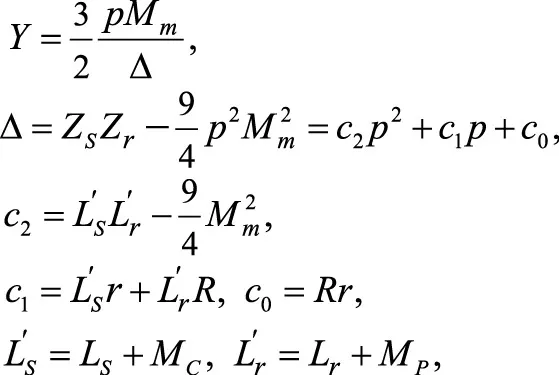
Uq, q = 1, 2, 3 — изображения напряжений по Лапласу.
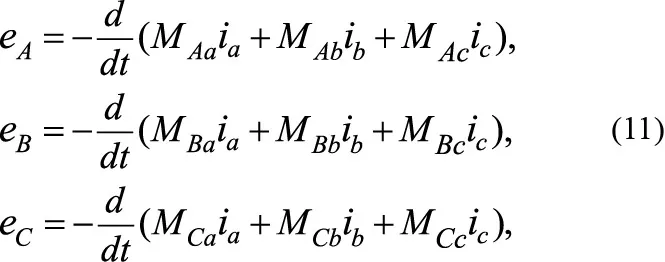
С помощью выражений (36) амплитуды фазных токов статора ISmи токи ротора Irm:

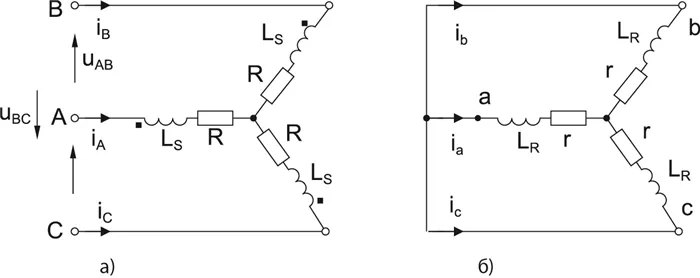
Обратным преобразованием Лапласа выражения (36) и подставив выражения для фазных токов в формулы моментов (7) и (8), получим аналитическое выражение для Mr(t) с ротором AD с задержкой. Чтобы избежать утомительных преобразований и громоздких формул, можно провести моделирование в системе Mathlab SIMULINK по структурной схеме, показанной на рис. 5.

Рисунок 5. Схематическое изображение отложенного АД.
Применение модели к анализу процессов в АД
Чтобы применить полученные результаты, мы рассмотрим гипотетический двигатель AD с малой мощностью, диаметром ротора D = 0,4 м и длиной l = 0,6 м. Установив среднюю плотность ротора несколько выше плотности железа и равной 8 × 10 3 кг/м 3, получим момент инерции ротора J = 3,84- p кгм 2. Учитывая шаг полюсов t = p D/ 6 = 209 мм и шаг зубьев 5 мм, можно выбрать число витков фазной обмотки ротора n = 40. В качестве грубого ориентира принимается, что фактическая площадь поперечного сечения провода обмотки S = 8 мм2, длина фазной обмотки lo= 2( D + l ) n = 80 м, удельное сопротивление меди при 75°C составляет 1/47 × 1 0-6 Ом-м 2, это дает приблизительное значение для сопротивления r = 0,2 Ом. С учетом воздушного зазора d = 3 мм, коэффициент намотки kоб= 0,95, что приводит к индуктивности 0,09 Гн для 2 основных фаз. Если предположить, что индуктивность утечки составляет 10 % от основной индуктивности, то получится Lr= 0,1 Гн. Для простоты мы предполагаем, что параметры обмоток статора и ротора одинаковы. Предполагается, что взаимная индуктивность обмоток статора и ротора равна основной индуктивности, т.е. Mm= 0.09 Gn, MС= MР= 0,045 Гн, так что L ‘s= L ‘r= 0,145R Гн, R = r = 0,2 Ом. Определив приблизительное значение коэффициента KB= m0n /2 d = 8,4 × 1 0-3 Тл/А, мы рассчитали KM(6) равна 0,0768 Нм/А 2 .
Для выбранных параметров АД с формулой (27) для Um= 311 В, w = 100p 1/c зависимость электромагнитного момента от абсолютного скольжения Mr( v ) На рисунке 6 показана зависимость Mrпротив относительного скольжения s = n / w .
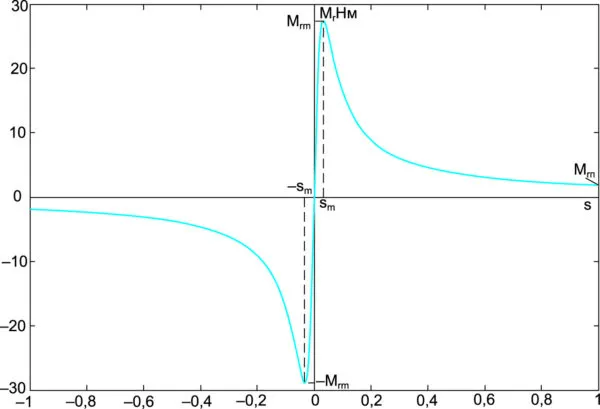
Рисунок 6: Зависимость электромагнитного момента Mr ротора от относительного скольжения s = v / w
С помощью формул (29) и (30) мы можем вывести vm=10.352 1/c, ( sm=0,033), Mrm=27,357 Нм. Если в формулу (27) подставить v = w, то получим Mrп=1,8489 Нм.
Использование полученной модели AD для анализа переходных процессов дает пример электромагнитного процесса, когда трехфазное напряжение амплитудой Um= 311 В и частоте w = 100 п 1/с при постоянной скорости синхронного ротора W = w и приложении момента нагрузки MН= 15 Нм после окончания электромагнитного переходного процесса. Перед окончанием электромагнитного переходного процесса электромагнитный момент Mrбыла отделена от двигателя в модели. Временные диаграммы MrW, ток статора и ток ротора: iA, iB, iC, ia, ib, ic(Рисунок 7). Моделирование было выполнено в MATHLAB 6.5 SIMULINK 5 методом ode 23 с относительной погрешностью 1 × 1 0-6.
Выводы
- Математическая модель АД, построенная без использования предположения о существовании кругового вращающегося поля в его воздушном зазоре и различных преобразований координат, подтверждает все основные свойства АД в переходных и установившихся режимах.
- Модель справедлива при любом характере изменения параметров трехфазной системы напряжений питания обмотки статора (частоты и величины напряжений).
3. разработанная цифровая модель двигателей АД позволяет исследовать изменения токов статора и ротора, электромагнитного момента и скорости вращения ротора в переходном и установившемся режимах и выбрать наиболее благоприятное соотношение между параметрами двигателя.
- Ковач К. П., Рац И. Переходные процессы в машинах переменного тока. Госэнергоиздат, 1963.
- Копылов И. П. Электрические машины. Учебник для вузов. М.: Энергоатомиздат, 1986.
- Соколовский Г. Г. Электроприводы переменного тока с частотным регулированием. Учебник для вузов. М.: Академия, 2006.
- Усольцев А. А. Частотное управление асинхронными двигателями. Учебное пособие. СПб., СПбГУ ИТМО, 2006.
- Коршунов А. И. Построение математической модели синхронного двигателя с постоянными магнитами на роторе // Электротехника. 2009. № 1.
- Коршунов А. И. Электромагнитный момент синхронного двигателя с постоянными магнитами // Известия вузов. Приборостроение. 2015. Т. 58. № 1.
Математическая модель асинхронного двигателя .
Принципиальная схема, асинхронный двигатель, уравнение, ток статора, проекционное уравнение, математическая модель, производная величина, номинальная работа, интегральная связь .
Асинхронный двигатель, ток статора, математическая модель, номинальная частота, номинальная работа, регулятор тока, проекция, общая цепь, базовое значение системы, электромагнитный момент .
Моделирование САР скорости системы «АИН ШИМ – АД».
Блок-схема, математическая модель, координатный преобразователь, асинхронный двигатель, ток статора, электромагнитный момент, число, передаточная функция, уравнение, проекция .
Элементы системы управления (CP, фильтр, контроллер) «привязаны» к вращающейся системе координат, а математическая модель линейного асинхронного двигателя — к фиксированной трехфазной системе индукторов.
Математическая модель АД в неподвижной системе координат .
Блок-схема, уравнение, система уравнений, электромагнитный импульс, часть уравнения, уравнение предположения, результат моделирования, фиксированная система координат, асинхронный двигатель .
Уравнение, система координат, структурная схема, система координат ротора, вектор, фиксированная система координат, асинхронный двигатель, электромагнитный момент .